
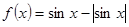 的性质,
的性质,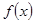 是以
是以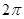 为周期的周期函数 ②
为周期的周期函数 ②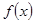 的单调递增区间为
的单调递增区间为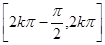 ,
,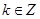
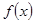 的值域为
的值域为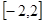 ④
④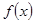 取最小值的
取最小值的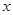 的取值集合为
的取值集合为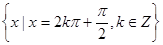
科目:高中数学 来源:不详 题型:解答题
|
|
2
| ||
| 5 |
2
| ||
| 5 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
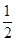 x(x+1)(41-2x)(x≤12且x∈N*)
x(x+1)(41-2x)(x≤12且x∈N*)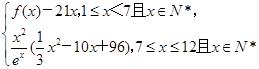
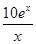 ,问:该商场销售A品牌商品,预计第几月的月利润达到最大值?月利润最大值是多少?(e6≈403)
,问:该商场销售A品牌商品,预计第几月的月利润达到最大值?月利润最大值是多少?(e6≈403)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com