
°æƒø°øƒ≥≥« –Œ™¡ÀΩ‚”ŒøÕ»À ˝µƒ±‰ªØπʬ…£¨Ã·∏þ¬√”Œ∑˛ŒÒ÷ ¡ø£¨ ’ºØ≤¢’˚¿Ì¡À2014ƒÍ1‘¬÷¡2016ƒÍ12‘¬∆⁄º‰‘¬Ω”¥˝”ŒøÕ¡ø(µ•Œª£∫ÕÚ»À)µƒ ˝æ𣨪Ê÷∆¡À»ÁÕºÀ˘ 浃’€œþÕº£Æ

∏˘æð∏√’€œþÕº£¨œ¬¡–Ω·¬€¥ÌŒÛµƒ «(°°°°)
A. ‘¬Ω”¥˝”ŒøÕ¡ø÷‘¬‘ˆº”
B. ƒÍΩ”¥˝”ŒøÕ¡ø÷ƒÍ‘ˆº”
C. ∏˜ƒÍµƒ‘¬Ω”¥˝”ŒøÕ¡ø∏þ∑Â∆⁄¥Û÷¬‘⁄7,8‘¬
D. ∏˜ƒÍ1‘¬÷¡6‘¬µƒ‘¬Ω”¥˝”ŒøÕ¡øœý∂‘”⁄7‘¬÷¡12‘¬£¨≤®∂Ø–‘∏¸–°£¨±‰ªØ±»Ωœ∆ΩŒ»
 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™Õ÷‘≤![]() µƒ¿Î–ƒ¬ Œ™
µƒ¿Î–ƒ¬ Œ™![]() £¨÷±œþx+y+1=0”ÎÕ÷‘≤Ωª”⁄P°¢Q¡Ωµ„£¨«“OP°ÕOQ£¨«Û∏√Õ÷‘≤∑Ω≥ãÆ
£¨÷±œþx+y+1=0”ÎÕ÷‘≤Ωª”⁄P°¢Q¡Ωµ„£¨«“OP°ÕOQ£¨«Û∏√Õ÷‘≤∑Ω≥ãÆ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄¿‚îABC©ÅFED÷–£¨°˜DEF”ΰ˜ABC∑÷± «¿‚≥§Œ™1”Î2µƒ’˝»˝Ω«–Œ£¨∆Ω√ÊABC°Õ∆Ω√ÊBCDE£¨Àƒ±þ–ŒBCDEŒ™÷±Ω«Ã𖌣¨BC°ÕCD£¨CD=1£¨NŒ™CE÷–µ„£¨ ![]() £Æ
£Æ 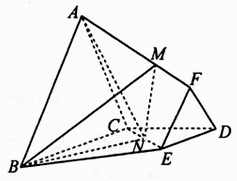
£®¢Ò£©¶ÀŒ™∫Œ÷µ ±£¨MN°Œ∆Ω√ÊABC£ø
£®¢Ú£©‘⁄£®¢Ò£©µƒÃıº˛œ¬£¨«Û÷±œþAN”Î∆Ω√ÊBMNÀ˘≥…Ω«µƒ’˝œ“÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄°˜ABC÷–£¨BC±þ…œµƒ∏þÀ˘‘⁄÷±œþµƒ∑Ω≥ÃŒ™x£≠2y£´1£Ω0£¨°œAµƒ∆Ω∑÷œþÀ˘‘⁄µƒ÷±œþ∑Ω≥ÃŒ™y£Ω0£Æ»Ùµ„Bµƒ◊¯±ÍŒ™(1,2)£¨«Ûµ„A∫Õµ„Cµƒ◊¯±Í£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø÷¥––»ÁÕºµƒ≥ÖÚøÚÕº£¨»Áπ˚ ‰»Îµƒa=6£¨b=4£¨ƒ«√¥ ‰≥ˆµƒsµƒ÷µŒ™£® £© 
A.17
B.22
C.18
D.20
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…ËÕ÷‘≤![]() £®
£®![]() £©µƒ”“Ωπµ„Œ™
£©µƒ”“Ωπµ„Œ™![]() £¨”“∂•µ„Œ™
£¨”“∂•µ„Œ™![]() £¨“—÷™
£¨“—÷™![]() £¨∆‰÷–
£¨∆‰÷–![]() Œ™‘≠µ„£¨
Œ™‘≠µ„£¨ ![]() Œ™Õ÷‘≤µƒ¿Î–ƒ¬ .
Œ™Õ÷‘≤µƒ¿Î–ƒ¬ .
£®¢Ò£©«ÛÕ÷‘≤µƒ∑Ω≥ãª
£®¢Ú£©…Ëπ˝µ„![]() µƒ÷±œþ
µƒ÷±œþ![]() ”ÎÕ÷‘≤Ωª”⁄µ„
”ÎÕ÷‘≤Ωª”⁄µ„![]() £®
£®![]() ≤ª‘⁄
≤ª‘⁄![]() ÷·…œ£©£¨¥π÷±”⁄
÷·…œ£©£¨¥π÷±”⁄![]() µƒ÷±œþ”Î
µƒ÷±œþ”Î![]() Ωª”⁄µ„
Ωª”⁄µ„![]() £¨”Î
£¨”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() £¨»Ù
£¨»Ù![]() £¨«“
£¨«“![]() £¨«Û÷±œþµƒ
£¨«Û÷±œþµƒ![]() –±¬ .
б .
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄Àƒ¿‚◊∂A©ÅBCFE÷–£¨Àƒ±þ–ŒEFCBŒ™Ã𖌣¨EF°ŒBC£¨«“EF= ![]() BC£¨°˜ABC «±þ≥§Œ™2µƒ’˝»˝Ω«–Œ£¨∂•µ„F‘⁄AC…œµƒ…‰”∞Œ™µ„G£¨«“FG=
BC£¨°˜ABC «±þ≥§Œ™2µƒ’˝»˝Ω«–Œ£¨∂•µ„F‘⁄AC…œµƒ…‰”∞Œ™µ„G£¨«“FG= ![]() £¨CF=
£¨CF= ![]() £¨BF=
£¨BF= ![]() £Æ
£Æ 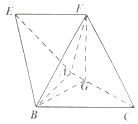
£®1£©÷§√˜£∫∆Ω√ÊFGB°Õ∆Ω√ÊABC£ª
£®2£©«Û∂˛√ÊΩ«E©ÅAB©ÅFµƒ”ýœ“÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™![]() µƒ∂•µ„
µƒ∂•µ„![]() £¨
£¨![]() ±þ…œµƒ÷–œþ
±þ…œµƒ÷–œþ![]() À˘‘⁄µƒ÷±œþ∑Ω≥ÃŒ™
À˘‘⁄µƒ÷±œþ∑Ω≥ÃŒ™![]() £¨
£¨![]() ±þ…œµƒ∏þ
±þ…œµƒ∏þ![]() À˘‘⁄÷±œþµƒ∑Ω≥ÃŒ™
À˘‘⁄÷±œþµƒ∑Ω≥ÃŒ™![]() £Æ
£Æ
£®![]() £©«Û
£©«Û![]() µƒ∂•µ„
µƒ∂•µ„![]() °¢
°¢![]() µƒ◊¯±Í£Æ
µƒ◊¯±Í£Æ
£®![]() £©»Ù‘≤
£©»Ù‘≤![]() æ≠π˝≤ªÕ¨µƒ»˝µ„
æ≠π˝≤ªÕ¨µƒ»˝µ„![]() °¢
°¢![]() °¢
°¢![]() £¨«“–±¬ Œ™
£¨«“–±¬ Œ™![]() µƒ÷±œþ”Α≤
µƒ÷±œþ”Α≤![]() œý«–”⁄µ„
œý«–”⁄µ„![]() £¨«Û‘≤
£¨«Û‘≤![]() µƒ∑Ω≥ãÆ
µƒ∑Ω≥ãÆ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø°∞æ∆∫Ûºð≥µ°±∫Õ°∞◊Ìæ∆ºð≥µ°±£¨∆‰ºÏ≤‚±Í◊º «ºð ª»À‘±—™“∫÷–µƒæ∆æ´∫¨¡ø![]() £®ºÚ≥∆—™æ∆∫¨¡ø£¨µ•Œª «∫¡øÀ/100∫¡…˝£©£¨µ±
£®ºÚ≥∆—™æ∆∫¨¡ø£¨µ•Œª «∫¡øÀ/100∫¡…˝£©£¨µ±![]() ±£¨Œ™æ∆∫Ûºð≥µ£ªµ±
±£¨Œ™æ∆∫Ûºð≥µ£ªµ±![]() ±£¨Œ™◊Ìæ∆ºð≥µ£Æƒ≥ –ΩªÕ®πпÌ≤ø√≈”⁄ƒ≥ÃÏÕÌ…œ8µ„÷¡11µ„…˵„Ω¯––“ª¥Œ¿π≤È––∂Ø£¨π≤“¿∑®≤È≥ˆ60√˚“˚æ∆∫ÛŒ•∑®ºð ªª˙∂Ø≥µ’þ£¨»ÁÕºŒ™’‚60√˚ºð ª‘±≥È—™ºÏ≤‚∫ÛÀ˘µ√Ω·π˚ª≠≥ˆµƒ∆µ¬ ∑÷≤º÷±∑ΩÕº£®∆‰÷–
±£¨Œ™◊Ìæ∆ºð≥µ£Æƒ≥ –ΩªÕ®πпÌ≤ø√≈”⁄ƒ≥ÃÏÕÌ…œ8µ„÷¡11µ„…˵„Ω¯––“ª¥Œ¿π≤È––∂Ø£¨π≤“¿∑®≤È≥ˆ60√˚“˚æ∆∫ÛŒ•∑®ºð ªª˙∂Ø≥µ’þ£¨»ÁÕºŒ™’‚60√˚ºð ª‘±≥È—™ºÏ≤‚∫ÛÀ˘µ√Ω·π˚ª≠≥ˆµƒ∆µ¬ ∑÷≤º÷±∑ΩÕº£®∆‰÷–![]() µƒ»À ˝º∆»Î
µƒ»À ˝º∆»Î![]() »À ˝÷ƃ⁄£©£Æ
»À ˝÷ƃ⁄£©£Æ

1£©«Û¥À¥Œ¿π≤È÷–◊Ìæ∆ºð≥µµƒ»À ˝£ª
2£©¥”Œ•∑®ºð≥µµƒ60»À÷–∞¥æ∆∫Ûºð≥µ∫Õ◊Ìæ∆ºð≥µ¿˚”√∑÷≤„≥È—˘≥È»°8»À◊ˆ—˘±æΩ¯––—–æø£¨‘Ÿ¥”≥È»°µƒ8»À÷–»Œ»°2»À£¨«Û¡Ω»À÷–«°”–1»À◊Ìæ∆ºð≥µµƒ∏≈¬ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com