
设f(x)=|x+1|+|x-3|.
(Ⅰ)解不等式f(x)≤3x+4;
(Ⅱ)若不等式f(x)≥m的解集为R,求实数m的取值范围.
(Ⅰ)不等式的解集为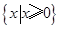 ;(Ⅱ)即
;(Ⅱ)即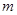 的取值范围为
的取值范围为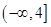 .
.
【解析】
试题分析:(Ⅰ)解不等式f(x)≤3x+4,首先将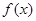 转化为分段函数
转化为分段函数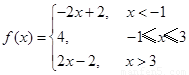 ,然后利用分段函数分段解不等式,从而求出不等式的解;易错点,不知将
,然后利用分段函数分段解不等式,从而求出不等式的解;易错点,不知将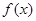 转化为分段函数;(Ⅱ)不等式
转化为分段函数;(Ⅱ)不等式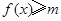 的解集为R,即当
的解集为R,即当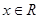 ,不等式
,不等式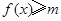 恒成立,只需求出
恒成立,只需求出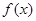 的最小值即可,此题可以利用分段函数求出最小值,也可利用绝对值不等式的性质来求最小值.
的最小值即可,此题可以利用分段函数求出最小值,也可利用绝对值不等式的性质来求最小值.
试题解析:(Ⅰ)因为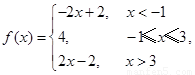 所以原不等式等价于
所以原不等式等价于
① 或②
或② 或③
或③ , 解得①无解,②
, 解得①无解,②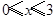 ,③
,③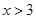 ,
,
因此不等式的解集为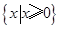 .
.
(Ⅱ)由于不等式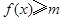 的解集为
的解集为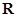 ,所以
,所以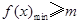 , 又
, 又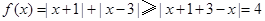 ,即
,即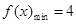 ,
所以
,
所以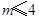 ,即
,即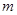 的取值范围为
的取值范围为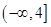 .
.
考点:绝对值不等式的解法,考查学生数形结合的能力以及化归与转化思想,以及学生的运算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014届河南省原名校联盟高三上学期第一次摸底考试理科数学试卷(解析版) 题型:解答题
设函数f(x)=|2x+1|-|x-2|.
(Ⅰ)求不等式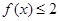 的解集;
的解集;
(Ⅱ)若{x|f(x)≥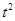 -t}∩{y|0≤y≤1}≠
-t}∩{y|0≤y≤1}≠ ,求实数t的取值范围.
,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届河南省原名校联盟高三上学期第一次摸底考试理科数学试卷(解析版) 题型:填空题
对于实数a,b,定义运算“﹡”:a﹡b=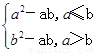 ,设f(x)=(2x-1)﹡x,且关于x 的方程f(x)=m(m∈R)恰有三个互不相等的实数根
,设f(x)=(2x-1)﹡x,且关于x 的方程f(x)=m(m∈R)恰有三个互不相等的实数根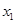 ,
,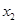 ,
,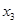 ,则
,则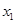 +
+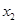 +
+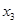 的取值范围是___________.
的取值范围是___________.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河南省商丘市高三第二次模拟考试数学理卷 题型:解答题
(本小题满分10分)选修4-5:不等式选讲
设函数f(x)=|x-1|+|x-2|.

(Ⅰ)画出函数y=f(x)的图象;
(Ⅱ)若不等式|a+b|-|a-b|≤|a|·f(x)对任意a,b∈R且a≠0恒成立,求实数x的范围
查看答案和解析>>
科目:高中数学 来源:2010年新课标版高一数学必修一第二章单元测试 题型:选择题
设f(x)=lg(10x+1)+ax是偶函数,g(x)=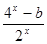 是奇函数,那么a+b的值为( )
是奇函数,那么a+b的值为( )
A.
1 B.-1 C.-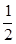 D.
D.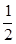
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com