
(文科只做(1)(2)问,理科全做)
设 是函数
是函数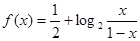 图象上任意两点,且
图象上任意两点,且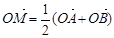 ,已知点
,已知点 的横坐标为
的横坐标为 ,且有
,且有 ,其中
,其中 且n≥2,
且n≥2,
(1)
求点 的纵坐标值;
的纵坐标值;
(2)
求 ,
, ,
, 及
及 ;
;
(3)已知 ,其中
,其中 ,且
,且 为数列
为数列 的前n项和,若
的前n项和,若 对一切
对一切 都成立,试求λ的最小正整数值。
都成立,试求λ的最小正整数值。
(1)M点的纵坐标为定值 ;
;
(2)
(3) 的最小正整数为1。
的最小正整数为1。
【解析】
试题分析:(1)依题意由 知M为线段AB的中点。
知M为线段AB的中点。
又 的横坐标为1,A
的横坐标为1,A ,B
,B 即
即

即M点的纵坐标为定值 (理3分) (文4分)
(理3分) (文4分)
(2) (文6分)
(文6分)
 (文8分)
(文8分)
 ……(文8分)(理2小题共5分)
……(文8分)(理2小题共5分)
由①知

 (文14分)
(文14分)
(3)当 时,
时,
又 ,
, 也适合。
也适合。 


由 恒成立
恒成立
而 (当且仅当
(当且仅当 取等号)
取等号)
 ,
, 的最小正整数为1(理14分)
的最小正整数为1(理14分)
考点:本题主要考查函数的概念,对数函数的图象和性质,数列的概念,不等式恒成立问题。
点评:难题,本题综合考查函数的概念,对数函数的图象和性质,数列的概念,不等式恒成立问题。难度较大,对于不等式恒成立问题,往往通过构造函数,确定函数的最值,使问题得解。


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:浙江省龙游中学2007届高三数学模拟练习卷(1) 题型:044
把圆周分成四等份,A是其中一个分点,动点P在四个分点上按逆时针方向前进,现投掷一个质地均匀的正四面体,它的四个面上分别写着1、2、3、4四个数字,P从A点出发,按照正四面体底面上的数字前进几个分点,转一周之前继续投掷.
Ⅰ.求点P恰好返回A点的概率.(文科只做第一问)
Ⅱ.(理做)在点P转一周恰能返回的所有结果中,用随机变量ξ表示点
P返回A点时的投掷次数,求ξ的分布列和期望.
查看答案和解析>>
科目:高中数学 来源:2013届浙江省临海市高二第二学期第一次月考数学试卷 题型:解答题
(6分)(文科只做(1),理科(1)和(2)都做)
(1)求证:  不可能成等差数列
不可能成等差数列
(2)用数学归纳法证明: 
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com