
 ��
�� ��
�� ����
���� ����
����
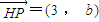 ��
��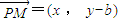 ��
��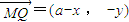 ����
����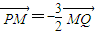 ����
����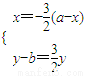 0���Ӷ�
0���Ӷ�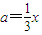 ��
��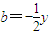 ����
����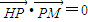 ����HP��PM���ɴ������M�Ĺ켣C��
����HP��PM���ɴ������M�Ĺ켣C��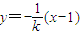 ����k��0������A��x1��y1����B��x2��y2������
����k��0������A��x1��y1����B��x2��y2������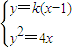 ����ky2-4y-4k=0����
����ky2-4y-4k=0����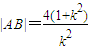 ��ͬ��|DE|=4��1+k2���ɴ�������ı���ADBE���S����Сֵ��
��ͬ��|DE|=4��1+k2���ɴ�������ı���ADBE���S����Сֵ��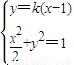 ���ã�1+2k2��x2-4k2x+2k2-2=0����
���ã�1+2k2��x2-4k2x+2k2-2=0����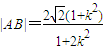 ��
��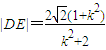 ���ɴ�������ı���ADBE���S����Сֵ��
���ɴ�������ı���ADBE���S����Сֵ��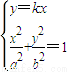 ���ã�b2+a2k2��x2-a2b2=0������
���ã�b2+a2k2��x2-a2b2=0������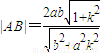 ��ͬ��
��ͬ��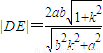 ���ɴ�������ı���ADBE���S����Сֵ��
���ɴ�������ı���ADBE���S����Сֵ��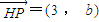 ��
��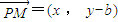 ��
�� ��������
��������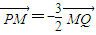 ��
��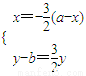 ����a��0���Ӷ�
����a��0���Ӷ�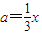 ��
��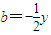 ����x��0��
����x��0��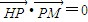 ����HP��PM��
����HP��PM��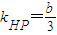 ����
����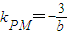 ��
��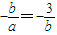 ��
��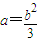 ����
����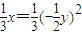 ��y2=4x��x��0����
��y2=4x��x��0����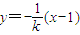 ����k��0��������A��x1��y1����B��x2��y2����
����k��0��������A��x1��y1����B��x2��y2����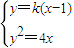 ����ȥx��������ky2-4y-4k=0��
����ȥx��������ky2-4y-4k=0��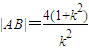 ��ͬ��|DE|=4��1+k2������7�֣�
��ͬ��|DE|=4��1+k2������7�֣�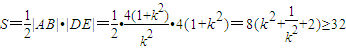 �����ҽ���k=±1ʱ�Ⱥų���������ı���ADBE���S����СֵΪ32����9�֣�
�����ҽ���k=±1ʱ�Ⱥų���������ı���ADBE���S����СֵΪ32����9�֣�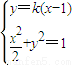 ���ã�1+2k2��x2-4k2x+2k2-2=0��
���ã�1+2k2��x2-4k2x+2k2-2=0��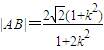 ��
��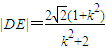 ����12�֣�
����12�֣�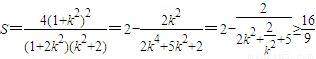 ��
��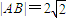 ��
��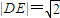 ����
����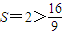 ���ʵ��ҽ���k2=1ʱ�ı���ADBE���S����Сֵ
���ʵ��ҽ���k2=1ʱ�ı���ADBE���S����Сֵ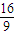 ����15�֣�
����15�֣�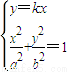 ��
��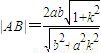 ��
��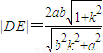 ����12�֣�
����12�֣�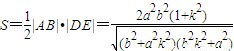 ������k2��0��
������k2��0��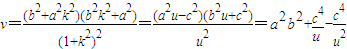 =
=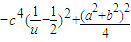 ������u��1����
������u��1����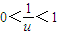 ���ʵ��ҽ���u=2����k2=1ʱ��v�����ֵ
���ʵ��ҽ���u=2����k2=1ʱ��v�����ֵ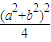 ����
����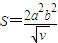 ����S����Сֵ
����S����Сֵ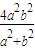 ���ʵ��ҽ���k=±1ʱ���ı���ADBE���S����СֵΪ
���ʵ��ҽ���k=±1ʱ���ı���ADBE���S����СֵΪ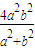 ����17�֣�
����17�֣�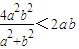 ���õ��ҽ���k=±1ʱ���ı���ADBE���S����СֵΪ
���õ��ҽ���k=±1ʱ���ı���ADBE���S����СֵΪ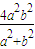 ����18�֣�
����18�֣�


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����֪��A��
��ͼ����֪��A��| 3 |
|
| OM |
| OH |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
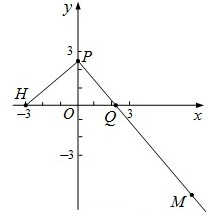 ��2009•¬������ģ����ͼ����֪��H��-3��0��������P��y���ϣ���Q��x���ϣ�������겻С���㣬��M��ֱ��PQ�ϣ�������
��2009•¬������ģ����ͼ����֪��H��-3��0��������P��y���ϣ���Q��x���ϣ�������겻С���㣬��M��ֱ��PQ�ϣ�������| HP |
| PM |
| PM |
| 3 |
| 2 |
| MQ |
| x2 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2009•¬������ģ����ͼ����֪��H��-3��0��������P��y���ϣ���Q��x���ϣ�������겻С���㣬��M��ֱ��PQ�ϣ�������
��2009•¬������ģ����ͼ����֪��H��-3��0��������P��y���ϣ���Q��x���ϣ�������겻С���㣬��M��ֱ��PQ�ϣ�������| HP |
| PM |
| PM |
| 3 |
| 2 |
| MQ |
| x2 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2009���Ϻ���¬�����߿���ѧ��ģ�Ծ����Ŀƣ��������棩 ���ͣ������
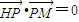 ��
��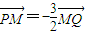 ��
��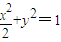 ��������2���еĶ���ȡΪ����F��1��0�������루2�������Ƶ�����Ľ⣮
��������2���еĶ���ȡΪ����F��1��0�������루2�������Ƶ�����Ľ⣮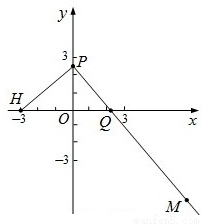
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com