练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

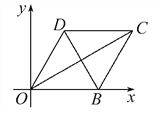
    【题目】如图，菱形OBCD的顶点O与坐标原点重合，一边在x轴的正半轴上，已知∠BOD=60°，求菱形各边和两条对角线所在直线的倾斜角及斜率.

    【答案】见解析

    【解析】试题分析：利用菱形的基本性质，即对边平行且相等，对角线平分每一组内对角，两条对角线互相垂直，先求倾斜角，再求斜率。

    试题解析：

    因为OD∥BC，∠BOD=60°，

    所以直线OD，BC的倾斜角都是60°，斜率都是tan60°=；

    又因为DC∥OB，

    所以直线DC，OB的倾斜角都是0°，斜率也都为0；

    由菱形的性质可得∠COB=30°，∠OBD=60°，

    所以直线OC的倾斜角为30°，斜率kOC=tan30°=，

    直线BD的倾斜角为∠DBx=180°-60°=120°，斜率。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】△ABC的三个顶点分别为A(0,4)、B(－2,6)、C(－8,0).

    (1)分别求边AC和AB所在直线的方程；

    (2)求AC边上的中线BD所在直线的方程；

    (3)求AC边的中垂线所在直线的方程；

    (4)求AC边上的高所在直线的方程；

    (5)求经过两边AB和AC的中点的直线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，椭圆E的左右顶点分别为A、B，左右焦点分别为F1、F2 ， |AB|=4，|F1F2|=2 ，直线y=kx+m（k＞0）交椭圆于C、D两点，与线段F1F2及椭圆短轴分别交于M、N两点（M、N不重合），且|CM|=|DN|．
    （Ⅰ）求椭圆E的离心率；
    （Ⅱ）若m＞0，设直线AD、BC的斜率分别为k1、k2 ， 求 的取值范围．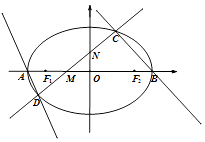

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，

    E是PC的中点．求证：

    （Ⅰ）CD⊥AE；

    （Ⅱ）PD⊥平面ABE．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆 为参数），A，B是C上的动点，且满足OA⊥OB（O为坐标原点），以原点O为极点，x轴的正半轴为极轴建立坐标系，点D的极坐标为 ．
    （1）求线段AD的中点M的轨迹E的普通方程；
    （2）利用椭圆C的极坐标方程证明 为定值，并求△AOB的面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥P－ABCD中，PA⊥底面ABCD，AD∥BC，AB＝AD＝AC＝3，PA＝BC＝4，M为线段AD上一点，AM＝2MD，N为PC的中点．

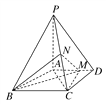
    (1)证明MN∥平面PAB；

    (2)求四面体N－BCM的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，BD是正方形ABCD的对角线，弧的圆心是A，半径为AB，正方形ABCD以AB为轴旋转，求图中Ⅰ，Ⅱ，Ⅲ三部分旋转所得旋转体的体积之比.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数，ω＞0，|φ|＜）的一个零点与之相邻的对称轴之间的距离为，且时f（x）有最小值．

    （1）求的解析式；

    （2）若，求f（x）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某数学教师对所任教的两个班级各抽取20名学生进行测试，分数分布如表，若成绩120分以上（含120分）为优秀．

    分数区间

    甲班频率

    乙班频率

    [0，30）

    0.1

    0.2

    [30，60）

    0.2

    0.2

    [60，90）

    0.3

    0.3

    [90，120）

    0.2

    0.2

    [120，150]

    0.2

    0.1

    优秀

    不优秀

    总计

    甲班

    乙班

    总计

    k0

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    P（K2≥k0）

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    （Ⅰ）求从乙班参加测试的90分以上（含90分）的同学中，随机任取2名同学，恰有1人为优秀的概率；
    （Ⅱ）根据以上数据完成上面的2×2列联表：在犯错概率小于0.1的前提下，你是否有足够的把握认为学生的数学成绩是否优秀与班级有关？

    查看答案和解析>>

    同步练习册答案