【题目】已知数列{an}及fn（x）=a1x+a2x2+…+anxn ， fn（﹣1）=（﹣1）nn，n=1，2，3，…
（1）求a1 ， a2 ， a3的值；
（2）求数列{an}的通项公式；
（3）求证： 
．
【答案】
（1）解：由已知f1（﹣1）=﹣a1=﹣1，所以a1=1．
f2（﹣1）=﹣a1+a2=2，所以a2=3．
f3（﹣1）=﹣a1+a2﹣a3=﹣3，所以a3=5
（2）解：令x=﹣1，则 
①
②
两式相减，得 
，
所以an+1=（n+1）+n．即an+1=2n+1．
又a1=1也满足上式，
所以数列{an}的通项公式为an=2n﹣1．（n=1，2，3…）
（3）证明： 
，
所以 
．③
．④
①﹣②，得 
= 
，
∴ 
．
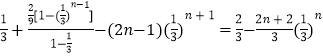又n=1，2，3…，∴ 
故 
＜1．
又 
∴ 
是递增数列，故 
…（11分）
∴ 
【解析】（1）由已知条件利用函数的性质能求出a1，a2，a3的值，（2）由已知条件进行错位相减能得出an+1=2n+1，进而得到数列{an}的通项公式，（3）利用错位相减法即可证明出结论.
科目：高中数学 来源： 题型：
【题目】如图，在由圆O：x2+y2=1和椭圆C： 
=1（a＞1）构成的“眼形”结构中，已知椭圆的离心率为 
，直线l与圆O相切于点M，与椭圆C相交于两点A，B． 
（1）求椭圆C的方程；
（2）是否存在直线l，使得 
= 
，若存在，求此时直线l的方程；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知曲线C1：（x﹣1）2+y2=1与曲线C2：y（y﹣mx﹣m）=0，则曲线C2恒过定点；若曲线C1与曲线C2有4个不同的交点，则实数m的取值范围是
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=aln（x+1）+ 
x2﹣x，其中a为非零实数．
（1）讨论函数f（x）的单调性；
（2）若y=f（x）有两个极值点x1 ， x2 ， 且x1＜x2 ， 求证： 
＜ ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四边形ABCD中，AB=AC=AD，AH⊥CD于H，BD交AH于P，且PC⊥BC 
（1）求证：A，B，C，P四点共圆；
（2）若∠CAD= 
，AB=1，求四边形ABCP的面积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知复数z＝1＋mi（i是虚数单位，m∈R），且 
为纯虚数（ 
是z的共轭复数）．
（1）设复数 
，求|z1|；
（2）设复数 
，且复数z2所对应的点在第四象限，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知△BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，∠ADB=60°，E、F分别是AC、AD上的动点，且
（1）求证：不论
为何值，总有平面BEF⊥平面ABC；
（2）当λ为何值时，平面BEF⊥平面ACD ?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
