
分析 (1)根据函数单调性的定义进行证明即可.
(2)根据函数奇偶性的定义进行证明即可.
解答 解:(1)证明:设x1,x2∈(0,1)且x1<x2,
则f(x1)-f(x2)=$\frac{1}{{x}_{1}}$+x1-($\frac{1}{{x}_{2}}$+x2)=$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$+(x1-x2)=(x1-x2)•$\frac{{x}_{1}{x}_{2}-1}{{x}_{1}{x}_{2}}$,
∵x1-x2<0,0<x1x2<1,x1x2-1<0,
∴f(x1)-f(x2)>0,即f(x1)>f(x2),
则函数f(x)在(0,1)上的单调递减.
(2)函数的定义域为{x|x≠0},
则f(-x)=-x-$\frac{1}{x}$=-(x+$\frac{1}{x}$)=-f(x),
则函数f(x)是奇函数.
点评 本题主要考查函数奇偶性和单调性的判断,利用函数单调性和奇偶性的定义是解决本题的关键.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
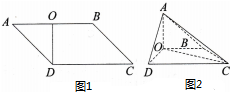 如图1,在∠A=45°的平行四边形ABCD中,DO垂直平分AB,且AB=2,现将△ADO沿DO折起(如图2),使AC=$\sqrt{6}$.
如图1,在∠A=45°的平行四边形ABCD中,DO垂直平分AB,且AB=2,现将△ADO沿DO折起(如图2),使AC=$\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com