
已知|a|=1,a·b=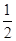 ,(a-b)·(a+b)=
,(a-b)·(a+b)=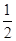 ,
,
求:(1)a与b的夹角;
(2)a-b与a+b的夹角的余弦值.
(1)θ=45°;(2)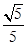 .
.
【解析】本试题主要是考查了向量的数量积的公式的运用以及性质中求夹角和模长的综合运用。
(1)中结合题中的条件|a|=1,a·b=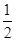 ,(a-b)·(a+b)=
,(a-b)·(a+b)=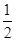 ,利用向量的数量积展开得到向量b的模,结合夹角公式得到结论。
,利用向量的数量积展开得到向量b的模,结合夹角公式得到结论。
(2)中利用数量积求解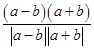 ,然后得到夹角关系式,得解。
,然后得到夹角关系式,得解。
解:(1)∵ (a-b)·(a+b)=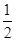 ,∴ |a|2-|b|2=
,∴ |a|2-|b|2=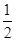 ,又∵ |a|=1,∴ |b|=
,又∵ |a|=1,∴ |b|=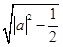 =
=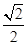 .
.
设a与b的夹角为θ,则cosθ=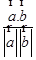 =
=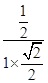 =
=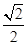 , ∴ θ=45°.
, ∴ θ=45°.
(2)∵ (a-b)2=a2-2a·b+b2=1-2×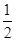 +
+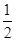 =
=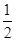 ,∴ |a-b|=
,∴ |a-b|=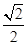 .
.
(a+b)2=a2+2a·b+b2=1+2×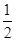 +
+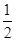 =
= ,∴ |a+b|=
,∴ |a+b|=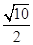 ,设a-b与a+b的夹角为α,则cosα=
,设a-b与a+b的夹角为α,则cosα=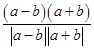 =
=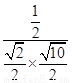 =
=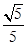 .
.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源:学习高手必修四数学苏教版 苏教版 题型:013
已知a=(1,1),b=(1,0)且ka+b恰好与b垂直,则实数k的值是
1
-1
1或-1
以上都不对
查看答案和解析>>
科目:高中数学 来源:山东省任城一中2010-2011学年高二下学期期末考试数学文科试题 题型:013
已知A,B均为集合U={1,3,5,7,9}的子集,且A∩B={3},(?UB)∩A={9},则A=
{1,3}
{3,7,9}
{3,5,9}
{3,9}
查看答案和解析>>
科目:高中数学 来源: 题型:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com