
| A. | sin$\frac{19π}{8}$<cos$\frac{14π}{9}$ | B. | sin(-$\frac{54π}{7}$)<sin(-$\frac{63π}{8}$) | ||
| C. | tan(-$\frac{13π}{4}$)>tan(-$\frac{17π}{5}$) | D. | tan138°>tan143° |
分析 根据诱导公式,结合正弦函数和正切函数的单调性,可得答案.
解答 解:sin$\frac{19π}{8}$=sin$\frac{3π}{8}$>cos$\frac{14π}{9}$=cos$\frac{4π}{9}$=sin$\frac{π}{18}$,故A错误;
sin(-$\frac{54π}{7}$)=sin$\frac{2π}{7}$>sin(-$\frac{63π}{8}$)=sin$\frac{π}{8}$,故B错误;
tan(-$\frac{13π}{4}$)=tan$\frac{3π}{4}$>tan(-$\frac{17π}{5}$)=tan$\frac{3π}{5}$,故C正确;
tan138°<tan143°,故D错误;
故选:C.
点评 本题考查的知识点是三角函数值大小比较,正弦函数和正切函数的单调性,诱导公式,难度中档.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 金额分组 | [1,5) | [5,9) | [9,13) | [13,17) | [17,21) | [21,25] |
| 频数 | 3 | 9 | 17 | 11 | 8 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
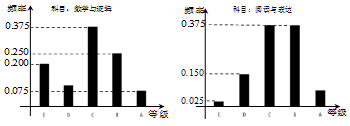
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com