
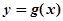 满足:g(2)=4,定义域为
满足:g(2)=4,定义域为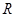 的函数
的函数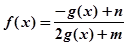 是奇函数。
是奇函数。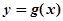 的解析式;(2)求m,n的值;
的解析式;(2)求m,n的值;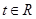 ,不等式
,不等式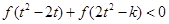 恒成立,求实数
恒成立,求实数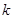 的取值范围
的取值范围 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源:不详 题型:单选题
 在区间
在区间 上有定义, 若
上有定义, 若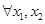
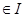 , 都有
, 都有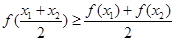 , 则称
, 则称 是区间
是区间 的向上凸函数;若
的向上凸函数;若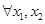
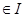 , 都有
, 都有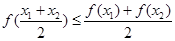 , 则称
, 则称 是区间
是区间 的向下凸函数. 有下列四个判断:
的向下凸函数. 有下列四个判断: 是区间
是区间 的向上凸函数,则
的向上凸函数,则 是区间
是区间 的向下凸函数;
的向下凸函数; 和
和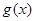 都是区间
都是区间 的向上凸函数, 则
的向上凸函数, 则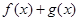 是区间
是区间 的向上凸函数;
的向上凸函数; 在区间
在区间 的向下凸函数且
的向下凸函数且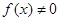 ,则
,则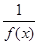 是区间
是区间 的向上凸函数;
的向上凸函数; 是区间
是区间 的向上凸函数,
的向上凸函数,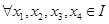 , 则有
, 则有
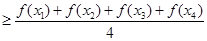
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
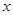 小时的收费为
小时的收费为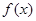 元
元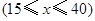 ,在乙家租一张球台开展活动
,在乙家租一张球台开展活动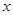 小时的收费为
小时的收费为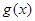 元
元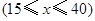 .试求
.试求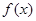 和
和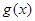 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
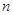 个月的维修费为
个月的维修费为 元,买这种冰激凌机花费
元,买这种冰激凌机花费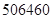 元,使用
元,使用 年报废,那么这台冰激凌机从投入使用到报废,每天的消耗是( )
年报废,那么这台冰激凌机从投入使用到报废,每天的消耗是( ) 机器从投入生产到报废共付出的维修费用与购买费用之和平均到每一天叫做每天的消耗;
机器从投入生产到报废共付出的维修费用与购买费用之和平均到每一天叫做每天的消耗;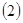 一年按
一年按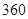 天计算.)
天计算.)A.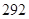 元 元 | B.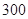 元 元 | C.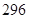 元 元 | D.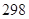 元 元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com