
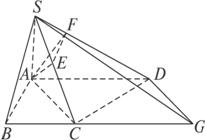
(1)求证:平面CSD⊥平面SAC;
(2)求点A到平面SCD的距离;
(3)求二面角ASDC的大小;
(4)求直线SD与AC所成的角.
(1)证明:由∠ABC=90°,得AC=![]() a,CD=
a,CD=![]() a,AC2+CD2=AD2.
a,AC2+CD2=AD2.
∴∠ACD=90°.
又SA⊥CD,
∴CD⊥平面SAC.
∴平面DSC⊥平面SAC.
(2)解析:过点A作AE⊥SC,E为垂足,则AE⊥平面SCD,SC=![]() a.
a.
∴AE=![]() ,即A到平面SCD的距离为
,即A到平面SCD的距离为![]() a.
a.

(3)解析:作EF⊥SD,垂足为F,则AF⊥SD.∴∠AFE为二面角A-SD-C的平面角.
又AE⊥EF,SD=![]() a,
a,
AF=![]() ,
,
∴sin∠AFE=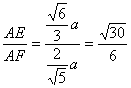 ,
,
即二面角A-SD-C为arcsin![]() .
.
(4)解析:延长BC至G,使GC=![]() a,AG=
a,AG=![]() a,SG=
a,SG=![]() a,
a,
cos∠SDG=![]() ,
,
∴SD与AC所成的角为arccos![]() .
.


科目:高中数学 来源: 题型:
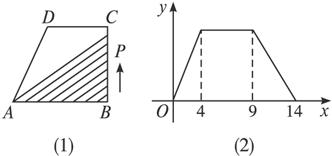
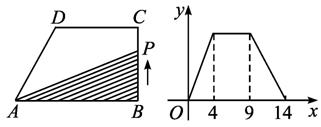
 有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图),∠ABC=45°,AB=AD=1,DC⊥BC,则这块菜地的面积为
有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图),∠ABC=45°,AB=AD=1,DC⊥BC,则这块菜地的面积为
| ||
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
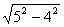
A.10 B.16 C.18 D.32
查看答案和解析>>
科目:高中数学 来源: 题型:
A.10 B.16 C.18 D.32
查看答案和解析>>
科目:高中数学 来源: 题型:
(1) (2)
A.10 B.16 C.18 D.32
查看答案和解析>>
科目:高中数学 来源: 题型:
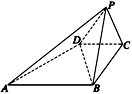
如图所示,已知四棱锥P—ABCD的底面是直角梯形,∠ABC=∠BCD=90°,
AB=BC=PB=PC=2CD,侧面PBC⊥底面ABCD.证明:
(1)PA⊥BD;
(2)平面PAD⊥平面PAB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com