
| A. | a1+a2+a3+a4=0 | |
| B. | |a1+a2+a3+a4|=2或2$\sqrt{2}$ | |
| C. | ai(i=1,2,3,4)中任意两个都是一对单位正交向量 | |
| D. | a1,a4是一对单位正交向量 |
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽豪州蒙城县一中高二上月考一数学试卷(解析版) 题型:解答题
设数列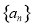 的前
的前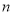 项和为
项和为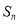 ,
,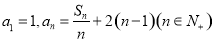 .
.
(1)证明:数列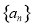 为等差数列,并分别求出
为等差数列,并分别求出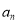 和
和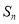 ;
;
(2)设数列 的前
的前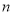 项和为
项和为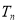 ,证明:
,证明: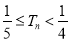 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 27 | B. | 16 | C. | 9 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | an=$\frac{2}{3}$n+$\frac{1}{3}$ | B. | an=$\frac{2}{3}$n-$\frac{1}{3}$ | C. | an=$\frac{1}{3}$n+$\frac{1}{3}$ | D. | an=$\frac{2}{3}$n+$\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (5,6) | B. | (4,5) | C. | (3,4) | D. | (2,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com