
已知函数![]() .
.
(Ⅰ) 当![]() 时,求函数
时,求函数![]() 的单调区间和极值;
的单调区间和极值;
(Ⅱ) 若![]() 在
在![]() 上是单调增函数,求实数a的取值范围.
上是单调增函数,求实数a的取值范围.
解析: (Ⅰ) 易知,函数![]() 的定义域为
的定义域为![]() . ………………………1分w.w.w.k.s.5.u.c.o.m
. ………………………1分w.w.w.k.s.5.u.c.o.m ![]()
当![]() 时,
时,![]() . ………………………3分
. ………………………3分
当x变化时,![]() 和
和![]() 的值的变化情况如下表:
的值的变化情况如下表:
x | (0,1) | 1 | (1,+∞) |
| - | 0 | + |
| 递减 | 极小值 | 递增 |
………………………5分
由上表可知,函数![]() 的单调递减区间是(0,1)、单调递增区间是(1,+∞)、极小值是
的单调递减区间是(0,1)、单调递增区间是(1,+∞)、极小值是![]() . ………………………7分w.w.w.k.s.5.u.c.o.m
. ………………………7分w.w.w.k.s.5.u.c.o.m ![]()
(Ⅱ) 由![]() ,得
,得![]() . ………………………9分
. ………………………9分
若函数![]() 为
为![]() 上的单调增函数,则
上的单调增函数,则![]() 在
在![]() 上恒成立,即不等式
上恒成立,即不等式![]() 在
在![]() 上恒成立.也即
上恒成立.也即![]() 在
在![]() 上恒成立. ………11分
上恒成立. ………11分
令![]() ,则
,则![]() . w.w.w.k.s.5.u.c.o.m
. w.w.w.k.s.5.u.c.o.m ![]()
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为减函数,
上为减函数,
![]() . ………………………………………………13分
. ………………………………………………13分
所以![]() .
.
∴![]() 的取值范围为
的取值范围为![]() . ………………………14分
. ………………………14分


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:
已知函数![]() (1)当a=4,
(1)当a=4,![]() ,求函数f(x)的最大值;(2)若x≥a , 试求f(x)+3 >0 的解集;(3)当
,求函数f(x)的最大值;(2)若x≥a , 试求f(x)+3 >0 的解集;(3)当![]() 时,f(x)≤2x – 2 恒成立,求实数a的取值范围.
时,f(x)≤2x – 2 恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省济宁市泗水一中高三(上)期末数学模拟试卷(理科)(解析版) 题型:选择题
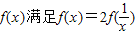 ,当x∈[1,3]时,f(x)=lnx,若在区间
,当x∈[1,3]时,f(x)=lnx,若在区间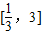 内,函数g(x)=f(x)-ax,有三个不同的零点,则实数a的取值范围是( )
内,函数g(x)=f(x)-ax,有三个不同的零点,则实数a的取值范围是( )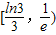
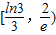
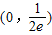
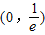
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省晋江市四校高三第二次联合考试文科数学试卷 题型:选择题
已知函数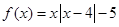 ,则当方程
,则当方程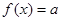 有三个不同实根时,实数
有三个不同实根时,实数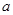 的取值范围
是 ( )
的取值范围
是 ( )
A. B.
B.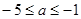 C.
C.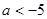 D.
D.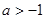
查看答案和解析>>
科目:高中数学 来源:2011-2012年山东省济宁市高二上学期期中考试文科数学 题型:解答题
(本小题满分12分)
已知函数f(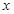 )=
)= ,当
,当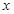 ∈(-2,6)时,其值为正,而当
∈(-2,6)时,其值为正,而当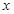 ∈(-∞,-2)∪(6,+∞)时,其值为负
∈(-∞,-2)∪(6,+∞)时,其值为负
(I)
求实数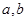 的值及函数f(
的值及函数f(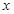 )的解析式
)的解析式
(II)设F(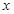 )= -
)= -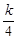 f(
f(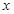 )+4
)+4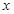 +12
+12 ,问
,问 取何值时,方程F(
取何值时,方程F(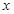 )=0有正根?
)=0有正根?
查看答案和解析>>
科目:高中数学 来源:2010年重庆市高一上学期期中考试数学试题 题型:解答题
(本小题满分10分)
已知函数 ,当点 (x,y)
是函数y = f (x) 图象上的点时,点
,当点 (x,y)
是函数y = f (x) 图象上的点时,点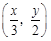 是函数y =
g(x) 图象上的点.
是函数y =
g(x) 图象上的点.
(1) 写出函数y = g (x) 的表达式;
(2)
当g(x)-f (x)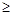 0时,求x的取值范围;
0时,求x的取值范围;
(3)
当x在 (2) 所给范围内取值时,求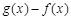 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com