练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知三角形三边边长分别为a、b、c，则三角形的面积为S＝，其中p＝．这个公式被称为海伦－秦九韶公式．已知一个三角形的三边边长分别为2、3、4，利用海伦－秦九韶公式设计一个算法，求出它的面积，画出算法的流程图．

    答案：
    解析：

    　　解：具体算法如下：

    　　S1　给出a，b，c的值，计算p＝；

    　　S2　计算三角形的面积S＝．

    　　算法流程图如图所示：


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    记实数x1，x2…xn中的最大数为max{x1，x2…xn}，最小数为min{x1，x2…xn}．已知△ABC的三边边长为a，b，c（a≤b≤c），定义它的倾斜度为t=max{
    a
    b
    ，
    b
    c
    ，
    c
    a
    }•min{
    a
    b
    ，
    b
    c
    ，
    c
    a
    }，则“t=1”是“△ABC为等边三角形”的
     
    ．（填充分不必要条件、必要不充分条件、充要条件、既不充分也不必要条件）．

    查看答案和解析>>

    科目：高中数学 来源：江西省会昌中学2011届高三第一次月考文科数学试题 题型：022

    记实数x1，x2，…xn中的最大数为max{x1，x2，…xn}，最小数为min{x1，x2，…xn}．已知△ABC的三边边长为a、b、c(a≤b≤c)，定义它的倾斜度为t＝max{，，}·min{，，}，则“t＝1”是“△ABC为等边三角形”的________．(填充分不必要条件、必要不充分条件、充要条件、既不充分也不必要条件)

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年重庆市三峡名校联盟高三12月联考理科数学试卷（解析版） 题型：解答题

    （本小题满分12分）已知直角的三边长,满足 

    (1)已知均为正整数,且成等差数列,将满足条件的三角形的面积从小到大排成一列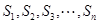,且,求满足不等式的所有的值;

    (2)已知成等比数列,若数列满足,证明数列中的任意连续三项为边长均可以构成直角三角形,且是正整数.

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年江西省七校高三上学期第一次联考文科数学试卷（解析版） 题型：填空题

    记实数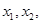…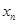中的最大数为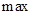{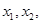…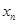}，最小数为min{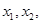…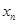}.已知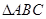的三边边长为、、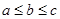（）,定义它的倾斜度为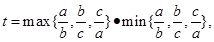则“t=1”是“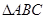为等边三角形”的            。

    （填充分不必要条件、必要不充分条件、充要条件、既不充分也不必要条件）

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年重庆市高三第五次月考理科数学 题型：选择题

    已知点P是边长为1的正三角形内一点，该点到三角形三边的距离分别是a，b，c（），则的取值范围是（    ）

    A．                 B．                 C．               D．

     

     

    查看答案和解析>>

    同步练习册答案