
(满分14分)一个同心圆形花坛,分为两部分,中间小圆部分种植草坪和绿色灌木,周围的圆环分为n(n≥3,n∈N)等份,种植红、黄、蓝三色不同的花,要求相邻两部分种植不同颜色的花.
(1)如图1,圆环分成的3等份为a1,a2,a3,有多少不同的种植方法?如图2,圆环分成的4等份为a1,a2,a3,a4,有多少不同的种植方法?
(2)如图3,圆环分成的n等份为a1,a2,a3,……,an,有多少不同的种植方法?
|
[来源:学#科#网Z#X#X#K]
(1)18 (2)![]()
(1)如图1,先对a1部分种植,有3种不同的种法,再对a2、a3种植,
因为a2、a3与![]() a1不同颜色,a2、a3也不同.
a1不同颜色,a2、a3也不同.
所以S(3)=3×2=6(种)……………3分
如图2,S(4)=3×2×2×2-S(3)=18(种) ……………………………6分
![]() (2)如图3,圆环分为n等份,对a1有3种不同的种法,对a2、a3、…、an都有两种不同的种法,但这样的种法只能保证a1与ai(i
(2)如图3,圆环分为n等份,对a1有3种不同的种法,对a2、a3、…、an都有两种不同的种法,但这样的种法只能保证a1与ai(i![]() =2、3、……、n-1)不同颜色,但不能保证a1与an不同颜色.
=2、3、……、n-1)不同颜色,但不能保证a1与an不同颜色. ![]()
![]() ………………………………8
………………………………8![]() 分
分
于是一类是an与a1不同色的种法,这是符合要求的种法,记为![]() 种.另一类是an与a1同色的种法,这时可以把an与a1看成一部分,这样的种法相当于对n-1部分符合要求的种法,记为
种.另一类是an与a1同色的种法,这时可以把an与a1看成一部分,这样的种法相当于对n-1部分符合要求的种法,记为![]() .
.
共有3×2n-1种种法. ………………………………10分
这样就有![]() .即
.即![]() ,
,
则数列![]() 是首项为
是首项为![]() 公比为-1的等比数列.
公比为-1的等比数列.
则![]()
由⑴知:![]() ,∴
,∴![]() .
.
∴![]() . ………………………………13分[来源:学*科*网]
. ………………………………13分[来源:学*科*网]
答:符合要求的不同种法有![]() …………………14分
…………………14分


科目:高中数学 来源:2012-2013学年上海市徐汇区高三上学期期末考试理科数学试卷(解析版) 题型:解答题
(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
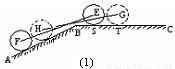
(理)某种型号汽车四个轮胎半径相同,均为 ,同侧前后两轮胎之间的距离(指轮胎中心之间距离)为
,同侧前后两轮胎之间的距离(指轮胎中心之间距离)为 (假定四个轮胎中心构成一个矩形). 当该型号汽车开上一段上坡路
(假定四个轮胎中心构成一个矩形). 当该型号汽车开上一段上坡路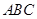 (如图(1)所示,其中
(如图(1)所示,其中 (
(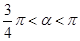 )),且前轮
)),且前轮 已在
已在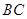 段上时,后轮中心在
段上时,后轮中心在 位置;若前轮中心到达
位置;若前轮中心到达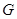 处时,后轮中心在
处时,后轮中心在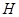 处(假定该汽车能顺利驶上该上坡路). 设前轮中心在
处(假定该汽车能顺利驶上该上坡路). 设前轮中心在 和
和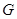 处时与地面的接触点分别为
处时与地面的接触点分别为 和
和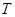 ,且
,且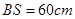 ,
,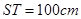 . (其它因素忽略不计)
. (其它因素忽略不计)
(1)如图(2)所示, 和
和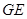 的延长线交于点
的延长线交于点 ,
,
求证: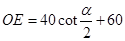 (cm);
(cm);
(2)当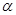 =
=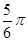 时,后轮中心从
时,后轮中心从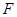 处移动到
处移动到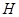 处实际移动了多少厘米? (精确到1cm)
处实际移动了多少厘米? (精确到1cm)
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省杭州市高三第二次教学质量考试数学理卷 题型:解答题
(本题满分14分)
如图1,在平面内,ABCD是 的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).
的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).


(Ⅰ) 设二面角E – AC – D1的大小为q,若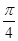 £ q £
£ q £  ,求线段BE长的取值范围;
,求线段BE长的取值范围;
(Ⅱ)在线段 上存在点
上存在点 ,使平面
,使平面 平面
平面 ,求
,求 与BE之间满足的关系式,并证明:当0 < BE < a时,恒有
与BE之间满足的关系式,并证明:当0 < BE < a时,恒有 <
1.
<
1.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分) 现有一个放有9个球的袋子,其中红球4个,白球3个,黄球2个,并且这些球除颜色外完全相同.
(Ⅰ) 现从袋子里任意摸出3个球,求其中有两球同色的概率;
(Ⅱ) 若在袋子里任意摸球,取后不放回,每次只摸出一球,直到摸出有两球同色为止,求摸球次数![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)
如图,在一条笔直的高速公路![]() 的同旁有两个城镇
的同旁有两个城镇![]() ,它们与
,它们与![]() 的距离分别是
的距离分别是![]() 与
与![]() ,
,![]() 在
在![]() 上的射影
上的射影![]() 之间距离为
之间距离为![]() ,现计划修普通公路把这两个城镇与高速公路相连接,若普通公路造价为
,现计划修普通公路把这两个城镇与高速公路相连接,若普通公路造价为![]() 万元/
万元/![]() ;而每个与高速公路连接的立交出入口修建费用为
;而每个与高速公路连接的立交出入口修建费用为![]() 万元.设计部门提交了以下三种修路方案:
万元.设计部门提交了以下三种修路方案:
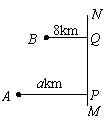 方案①:两城镇各修一条普通公路到高速公路,并各修一个立交出入口;
方案①:两城镇各修一条普通公路到高速公路,并各修一个立交出入口;
方案②:两城镇各修一条普通公路到高速公路上某一点![]() ,并
,并
在![]() 点修一个公共立交出入口;
点修一个公共立交出入口;
方案③:从![]() 修一条普通公路到
修一条普通公路到![]() ,再从
,再从![]() 修一条普通公路到
修一条普通公路到
高速公路,也只修一个立交出入口.
请你为这两个城镇选择一个省钱的修路方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)
如图1,在平面内,ABCD是![]() 的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).
的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).
(Ⅰ) 设二面角E – AC – D1的大小为q,若![]() £ q £
£ q £ ![]() ,求线段BE长的取值范围;
,求线段BE长的取值范围;

(第20题–1)

(第20题–2)
(Ⅱ)在线段![]() 上存在点
上存在点![]() ,使平面
,使平面![]() 平面
平面![]() ,求
,求![]() 与BE之间满足的关系式,并证明:当0 < BE < a时,恒有
与BE之间满足的关系式,并证明:当0 < BE < a时,恒有![]() < 1.
< 1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com