
已知随机变量 服从正态分布
服从正态分布 ,
,
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:填空题
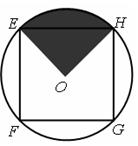
如图所示, 是以
是以 为圆心,半径为1的圆的内接正方形,将一粒豆子随机地扔到该圆内,用
为圆心,半径为1的圆的内接正方形,将一粒豆子随机地扔到该圆内,用 表示事件“豆子落在正方形
表示事件“豆子落在正方形 内”,
内”, 表示事件“豆子落在扇形
表示事件“豆子落在扇形 (阴影部分)内”,则
(阴影部分)内”,则 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
篮球运动员在比赛中每次罚球命中得1分,罚不中得0分,已知某运动员罚球命中的概率为0.7,则他罚球2次(每次罚球结果互不影响)的得分的数学期望是 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
两人相约在7:30到8:00之间相遇,早到者应等迟到者10分钟方可离去,如果两人出发是各自独立的,在7:30到8:00之间的任何时刻是等可能的,问两人相遇的可能性有多大 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
某人从标有1、2、3、4的四张卡片中任意抽取两张.约定如下:如果出现两个偶数或两个奇数,就将两数相加的和记为 ;如果出现一奇一偶,则将它们的差的绝对值记为
;如果出现一奇一偶,则将它们的差的绝对值记为 ,则随机变量
,则随机变量 的数学期望为 .
的数学期望为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com