
 -
- =1的离心率e>1+
=1的离心率e>1+ ,左、右焦点分别为F1、F2,左准线为l,能否在双曲线的左支上找一点P,使得|PF1|是P到l的距离d与|PF2|的等比中项?
,左、右焦点分别为F1、F2,左准线为l,能否在双曲线的左支上找一点P,使得|PF1|是P到l的距离d与|PF2|的等比中项?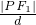 =
=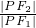 =e,即|PF2|=e|PF1|①
=e,即|PF2|=e|PF1|① ,|PF2|=
,|PF2|=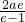 ,
, +
+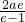 ≥2c.③
≥2c.③ ,由③得e2-2e-1≤0,
,由③得e2-2e-1≤0, ≤e≤1+
≤e≤1+ .
. 与已知e>1+
与已知e>1+ 矛盾.
矛盾. 与已知e>1+
与已知e>1+ 矛盾.从而断定在双曲线左支上找不到点P,使得|PF1|是P到l的距离d与|PF2|的等比中项.
矛盾.从而断定在双曲线左支上找不到点P,使得|PF1|是P到l的距离d与|PF2|的等比中项.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练19练习卷(解析版) 题型:填空题
已知双曲线 -
- =1的离心率为2,焦点与椭圆
=1的离心率为2,焦点与椭圆 +
+ =1的焦点相同,那么双曲线的焦点坐标为 ;渐近线方程为 .
=1的焦点相同,那么双曲线的焦点坐标为 ;渐近线方程为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com