
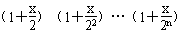 的展开式中,x的系数为an,x2的系数为bn,其中 n∈N*,
的展开式中,x的系数为an,x2的系数为bn,其中 n∈N*,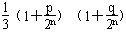 对n∈N*,n≥2恒成立?证明你的结论。
对n∈N*,n≥2恒成立?证明你的结论。 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
| x |
| 2 |
| x |
| 22 |
| x |
| 2n |
| 1 |
| 3 |
| p |
| 2n |
| q |
| 2n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 )(1+
)(1+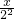 )…(1+
)…(1+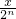 )的展开式中,x的系数为an,x2的系数为bn,其中 n∈N*.
)的展开式中,x的系数为an,x2的系数为bn,其中 n∈N*. (1+
(1+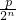 )(1+
)(1+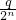 ) 对n∈N*,n≥2恒成立?证明你的结论.
) 对n∈N*,n≥2恒成立?证明你的结论.查看答案和解析>>
科目:高中数学 来源:2012年江苏省南京市高考数学二模试卷(解析版) 题型:解答题
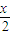 )(1+
)(1+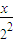 )…(1+
)…(1+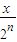 )的展开式中,x的系数为an,x2的系数为bn,其中 n∈N*.
)的展开式中,x的系数为an,x2的系数为bn,其中 n∈N*. (1+
(1+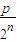 )(1+
)(1+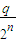 ) 对n∈N*,n≥2恒成立?证明你的结论.
) 对n∈N*,n≥2恒成立?证明你的结论.查看答案和解析>>
科目:高中数学 来源:2012年安徽省蚌埠二中高考数学一模试卷(文科)(解析版) 题型:解答题
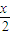 )(1+
)(1+ )…(1+
)…(1+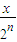 )的展开式中,x的系数为an,x2的系数为bn,其中 n∈N*.
)的展开式中,x的系数为an,x2的系数为bn,其中 n∈N*. (1+
(1+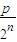 )(1+
)(1+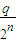 ) 对n∈N*,n≥2恒成立?证明你的结论.
) 对n∈N*,n≥2恒成立?证明你的结论.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com