
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,底面
,底面![]() 为矩形,
为矩形, ![]() 为
为![]() 中点,
中点, ![]() ,
, ![]() ,
, ![]() .
.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)设![]() 与
与![]() 的交点为
的交点为![]() ,连结
,连结![]() ,则
,则![]() 为
为![]() 的中点,由
的中点,由![]() 为
为![]() 中点,利用三角形中位线定理可得
中点,利用三角形中位线定理可得![]() ,从而根据线面平行的判定定理可得
,从而根据线面平行的判定定理可得![]() 平面
平面![]() ;(Ⅱ)由勾股定理可得
;(Ⅱ)由勾股定理可得![]() ,根据线面垂直的性质定理得
,根据线面垂直的性质定理得![]() 平面
平面![]() ,故
,故![]() ,再根据线面垂直的判定定理可得
,再根据线面垂直的判定定理可得![]() 平面
平面![]() ,故
,故![]() 就是直线
就是直线![]() 与平面
与平面![]() 所成的角,在直角
所成的角,在直角![]() 中可得
中可得![]() .
.
试题解析:
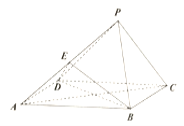
(Ⅰ)设![]() 与
与![]() 的交点为
的交点为![]() ,连结
,连结![]() .
.
因为![]() 为矩形,所以
为矩形,所以![]() 为
为![]() 的中点.
的中点.
在![]() 中,由已知
中,由已知![]() 为
为![]() 中点,所以
中点,所以![]() .
.
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)在![]() 中,
中, ![]() ,
, ![]() ,
,
所以![]() ,
,
即![]() .
.
因为平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
, ![]() ,
,
所以![]() 平面
平面![]() ,故
,故![]() .
.
又因为![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
故![]() 就是直线
就是直线![]() 与平面
与平面![]() 所成的角.
所成的角.
在直角![]() 中
中![]() ,
, ![]() ,
,
所以![]() .
.
即直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
【方法点晴】本题主要考查线面平行的判定定理、直线和平面成的角的定义及求法,属于难题. 证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.


科目:高中数学 来源: 题型:
【题目】十九大指出中国的电动汽车革命早已展开,通过以新能源汽车替代汽/柴油车,中国正在大力实施一项将重塑全球汽车行业的计划.2018年某企业计划引进新能源汽车生产设备,通过市场分析,全年需投入固定成本2500万元,每生产x(百辆),需另投入成本![]() 万元,且
万元,且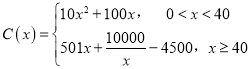 .由市场调研知,每辆车售价5万元,且全年内生产的车辆当年能全部销售完.
.由市场调研知,每辆车售价5万元,且全年内生产的车辆当年能全部销售完.
(1)求出2018年的利润L(x)(万元)关于年产量x(百辆)的函数关系式;(利润=销售额-成本)
(2)2018年产量为多少百辆时,企业所获利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线![]() 的焦点为
的焦点为![]() ,抛物线上一定点
,抛物线上一定点![]() .
.
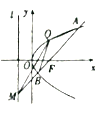
(1)求抛物线![]() 的方程及准线
的方程及准线![]() 的方程;
的方程;
(2)过焦点![]() 的直线(不经过
的直线(不经过![]() 点)与抛物线交于
点)与抛物线交于![]() 两点,与准线
两点,与准线![]() 交于点
交于点![]() ,记
,记![]() 的斜率分别为
的斜率分别为![]() ,问是否存在常数
,问是否存在常数![]() ,使得
,使得![]() 成立?若存在
成立?若存在![]() ,求出
,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[2018·赣中联考]李冶(1192-1279),真实栾城(今属河北石家庄市)人,金元时期的数学家、诗人,晚年在封龙山隐居讲学,数学著作多部,其中《益古演段》主要研究平面图形问题:求圆的直径、正方形的边长等.其中一问:现有正方形方田一块,内部有一个圆形水池,其中水池的边缘与方田四边之间的面积为13.75亩,若方田的四边到水池的最近距离均为二十步,则圆池直径和方田的边长分别是(注:240平方步为1亩,圆周率按3近似计算)( )
A. 10步,50步 B. 20步,60步 C. 30步,70步 D. 40步,80步
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着共享单车的成功运营,更多的共享产品逐步走入大家的世界,共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷.某公司随即抽取![]() 人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的
人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的![]() 人中的性别以及意见进行了分类,得到的数据如下表所示:
人中的性别以及意见进行了分类,得到的数据如下表所示:
男 | 女 | 总计 | |
认为共享产品对生活有益 |
|
|
|
认为共享产品对生活无益 |
|
|
|
总计 |
|
|
|
(1)根据表中的数据,能否在犯错误的概率不超过![]() 的前提下,认为对共享产品的态度与性别有关系?
的前提下,认为对共享产品的态度与性别有关系?
(2)现按照分层抽样从认为共享产品增多对生活无益的人员中随机抽取![]() 人,再从
人,再从![]() 人中随机抽取
人中随机抽取![]() 人赠送超市购物券作为答谢,求恰有
人赠送超市购物券作为答谢,求恰有![]() 人是女性的概率.
人是女性的概率.
参与公式: 
临界值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (实数
(实数![]() 为常数)
为常数)
(1)当![]() 时,证明
时,证明![]() 在
在![]() 上单调递减;
上单调递减;
(2)若![]() ,且
,且![]() 为偶函数,求实数
为偶函数,求实数![]() 的值;
的值;
(3)小金同学在求解函数![]() 的对称中心时,发现函数
的对称中心时,发现函数![]() 是一个复合函数,设
是一个复合函数,设![]() ,
,![]() ,则
,则![]() ,显然
,显然![]() 有对称中心,设为
有对称中心,设为![]() ,
,![]() 有反函数
有反函数![]() ,则
,则![]() 的对称中心为
的对称中心为![]() ,请问小金的做法是否正确?如果正确,请给出证明,并直接写出当
,请问小金的做法是否正确?如果正确,请给出证明,并直接写出当![]() 时
时![]() 的对称中心;如果错误,请举出反例,并用正确的方法直接写出当
的对称中心;如果错误,请举出反例,并用正确的方法直接写出当![]() 时
时![]() 的对称中心.
的对称中心.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com