
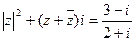 (i为虚数单位)
(i为虚数单位)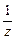 是实数,且-1<ω<2
是实数,且-1<ω<2
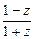 ,求证:u为纯虚数;(5分)
,求证:u为纯虚数;(5分) ,
, 且y=±
且y=±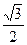 ,
, ±
±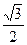 i.
i. =(a+
=(a+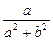 )+(b-
)+(b- )i
)i
 ,又∵b≠0,∴a2+b2=1,即|z|=1
,又∵b≠0,∴a2+b2=1,即|z|=1
 ,1)
,1)
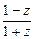 =
=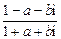 =
=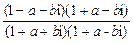 =
=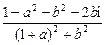
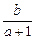 I,又∵a∈(-
I,又∵a∈(- ,1),b≠0,
,1),b≠0,
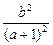 =2a+
=2a+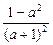 =2a-
=2a-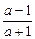
 =2[(a+1)+
=2[(a+1)+ ]-3
]-3
 ,1),∴a+1>0,
,1),∴a+1>0,  ≥2(当a+1=
≥2(当a+1= ,即a=0时,上式取等号.)
,即a=0时,上式取等号.)

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源:不详 题型:解答题
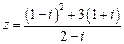 ,若
,若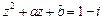 ,
,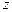 ;
; 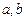 的值
的值查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com