④
分析：对a，b，c取特殊值可以排除①②③，要说明④正确，采用反证法的思想，由基本不等式得到a+
，b+
，c+
三个数的和大于等于6，假若a+
，b+
，c+
三个数均小于2，这与a+
，b+
，c+
三个数的和大于等于6矛盾．
解答：取a=b=c=1，则
．
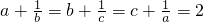
所以①②不正确；
取a=b=c=2，则a+
，b+
，c+
均大于2．
所以③不正确；
由a+
+b+
+c+
=
．
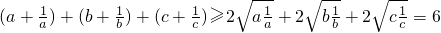
所以a+
，b+
，c+
三个正数中至少有一个不小于2，否则a+
+b+
+c+
＜6，矛盾．
故答案为④．
点评：本题考查了基本不等式，考查了命题真假的判定，要说明一个命题是假命题，举一反例即可，要说明一个命题为真命题，需要严格的理论证明，此题是基础题．
