
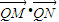 ×tan��MQN�Ƿ������ֵ��������������ֵ���������ʱֱ��l�ķ��̣��������ڣ��������ɣ�
×tan��MQN�Ƿ������ֵ��������������ֵ���������ʱֱ��l�ķ��̣��������ڣ��������ɣ�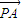 |��|
|��|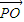 |��|
|��|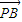 |�ɵȱ����У���
|�ɵȱ����У���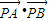 �ķ�Χ��
�ķ�Χ�� ×tan��MQN���ɵõ��ȼ۹�ϵ�����������������ȷ��Բ�ϵĵ㵽��֪�߶ε������룬�����ֱ��l�ķ��̣�
×tan��MQN���ɵõ��ȼ۹�ϵ�����������������ȷ��Բ�ϵĵ㵽��֪�߶ε������룬�����ֱ��l�ķ��̣� |��|
|��| |��|
|��| |�ɵȱ����У��õ���ȹ�ϵʽ��P��Բ�ڣ��õ�����ʽ���Ӷ������������ķ�Χ��
|�ɵȱ����У��õ���ȹ�ϵʽ��P��Բ�ڣ��õ�����ʽ���Ӷ������������ķ�Χ�� ×tan��MQN=
×tan��MQN= ×sin��MQN=2S��MQN
×sin��MQN=2S��MQN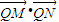 ×tan��MQN�����ֵΪ64����ʱֱ��l�ķ���Ϊ2x-y-5=0��
×tan��MQN�����ֵΪ64����ʱֱ��l�ķ���Ϊ2x-y-5=0�� |��|
|��|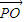 |��|
|��| |�ɵȱ����У���|
|�ɵȱ����У���| |2=|
|2=| |•|
|•| |��
|��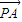 =��-5-x��-y����
=��-5-x��-y���� =��5-x��-y����
=��5-x��-y���� •
•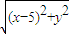 �������ã�x2-y2=
�������ã�x2-y2= ����x2=y2+
����x2=y2+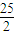 ��
�� ��
�� =��x2-25��+y2=2y2-
=��x2-25��+y2=2y2-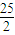
 ��[
��[ ��0����
��0����


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| y2 |
| 4 |
| OM |
| OA |
| OB |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����ƽ��ֱ������ϵxOy�У���ԲC��
��ͼ����ƽ��ֱ������ϵxOy�У���ԲC��| x2 |
| 2 |
| OT |
| OA |
| x0x |
| 2 |
| OP |
| OM |
| ON |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| OA |
| OB |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x2 |
| a2 |
| y2 |
| b2 |
| a |
| 2 |
| a |
| 2 |
| 3 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com