
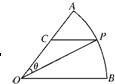
 如图,扇形AOB,圆心角AOB等于60°,半径为2,在弧AB上有一动点P,过P引平行于OB的直线和OA交于点C,设∠AOP=θ,求△POC面积的最大值及此时θ的值.
如图,扇形AOB,圆心角AOB等于60°,半径为2,在弧AB上有一动点P,过P引平行于OB的直线和OA交于点C,设∠AOP=θ,求△POC面积的最大值及此时θ的值. | OP |
| sin∠PCO |
| CP |
| sinθ |
| 2 |
| sin120° |
| CP |
| sinθ |
| 4 | ||
|
| OC |
| sin(60°-θ) |
| 2 |
| sin120° |
| 4 | ||
|
| 1 |
| 2 |
| 1 |
| 2 |
| 4 | ||
|
| 4 | ||
|
| ||
| 2 |
| 4 | ||
|
| 4 | ||
|
| ||
| 2 |
| 1 |
| 2 |
| 4 | ||
|
| ||
| 2 |
| 1 |
| 2 |
| 2 | ||
|
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 | ||
|
| 1 |
| 2 |
| ||
| 3 |


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:高中数学 来源: 题型:
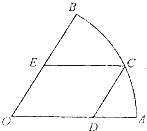
 如图,在半径为R、圆心角为
如图,在半径为R、圆心角为| π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在半径为R、圆心角为
如图,在半径为R、圆心角为| π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
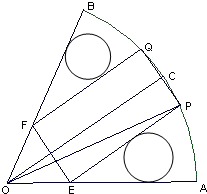
 (2013•南京二模)如图,某广场中间有一块扇形绿地OAB,其中O为扇形所在圆的圆心,∠AOB=60°,广场管理部门欲在绿地上修建观光小路:在
(2013•南京二模)如图,某广场中间有一块扇形绿地OAB,其中O为扇形所在圆的圆心,∠AOB=60°,广场管理部门欲在绿地上修建观光小路:在 | AB |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在半径为R、圆心角为
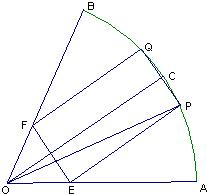
如图,在半径为R、圆心角为 的扇形金属材料中剪出一个长方形EPQF,并且EP与∠AOB的平分线OC平行,设∠POC=θ.
的扇形金属材料中剪出一个长方形EPQF,并且EP与∠AOB的平分线OC平行,设∠POC=θ.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com