
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 在同一坐标系中画出函数y=f(x)的图象和函数g(x)的图象,数形结合可得答案.
解答 解:∵函数y=f(x)(x∈R)满足f(x+2)=f(x),故函数y=f(x)是以2为坝基的周期函数,
又∵x∈(-1,1]时,f(x)=1-x2,
故函数y=f(x)的图象如下图所示: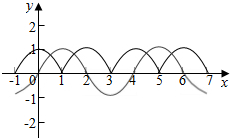
∵函数g(x)=Asinωx分别在两相邻对称轴x=1与x=-1处取得最大和最小值1与-1,
故函数g(x)的图象如上图所示:
由图可得:两个函数图象在区间[0,6]内共有4个交点,
故函数h(x)=f(x)-g(x)在区间[0,6]内零点的个数为4个,
故选:B
点评 本题考查的知识点是函数零点及零点个数的判定,数形结合思想,函数的图象和性质,难度中档.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:高中数学 来源: 题型:选择题
| A. | {1,$\frac{1}{2}$} | B. | {1,2} | C. | {0,1,2} | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 总计 | |
| 男生 | 40 | 20 | 60 |
| 女生 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| P(K2≥k) | 0.500 | 0.400 | 0.100 | 0.010 | 0.001 |
| k | 0.455 | 0.708 | 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
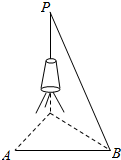 如图所示,要测量河对岸一电视塔的高PC,在河旁取A、B两点,测得AB=100$\sqrt{3}$米,∠CAB=∠ABC=60°,PB与地面所成的角为30°.
如图所示,要测量河对岸一电视塔的高PC,在河旁取A、B两点,测得AB=100$\sqrt{3}$米,∠CAB=∠ABC=60°,PB与地面所成的角为30°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A | B. | 2A | C. | $\frac{A}{2}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图是某圆拱桥的示意图,这个圆拱桥的水面跨度AB=24m,拱高OP=8m.问:为使宽为10m的船能从桥下顺利通过,应如何限制船体及装载的货物在水面以上的高度?
如图是某圆拱桥的示意图,这个圆拱桥的水面跨度AB=24m,拱高OP=8m.问:为使宽为10m的船能从桥下顺利通过,应如何限制船体及装载的货物在水面以上的高度?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com