
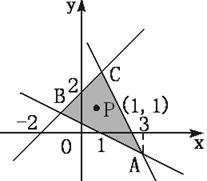
画出以A(3,-1)、B(-1,1)、C(1,3)为顶点的△ABC的区域(包括各边),写出该区域所表示的二元一次不等式组,并求以该区域为可行域的目标函数z=3x-2y的最大值和最小值![]()
如图,连结点A、B、C,则直线AB、BC、CA所围成的区域为所求△ABC区域![]()
直线AB的方程为x+2y-1=0,BC及CA的直线方程分别为x-y+2=0,2x+y-5=0![]()
在△ABC内取一点P(1,1),分别代入x+2y-1,x-y+2,2x+y-5
得x+2y-1>0,x-y+2>0,2x+y-5<0![]()
 因此所求区域的不等式组为
因此所求区域的不等式组为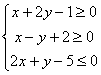
作平行于直线3x-2y=0的直线系3x-2y=t(t为参数),即平移直线y=![]() x,观察图形可知:当直线y=
x,观察图形可知:当直线y=![]() x-
x-![]() t过A(3,-1)时,纵截距-
t过A(3,-1)时,纵截距-![]() t最小
t最小![]() 此时t最大,tmax=3×3-2×(-1)=11;
此时t最大,tmax=3×3-2×(-1)=11;
当直线y=![]() x-
x-![]() t经过点B(-1,1)时,纵截距-
t经过点B(-1,1)时,纵截距-![]() t最大,此时t有最小值为tmin= 3×(-1)-2×1=-5
t最大,此时t有最小值为tmin= 3×(-1)-2×1=-5![]()
因此,函数z=3x-2y在约束条件
x+2y-1≥0,x-y+2≥0,2x+y-5≤0下的最大值为11,最小值为-5![]()
点评:确定一个点是否在不等式表示的区域内,只要将该点代入不等式,若满足该不等式,则点在区域内;若不满足不等式,则该点就不在区域内.
本例含三个问题:①画指定区域;②写所画区域的代数表达式——不等式组;③求以所写不等式组为约束条件的给定目标函数的最值![]()


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 (必修3做)设计一个求
(必修3做)设计一个求| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 99×100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 (必修3做)设计一个求
(必修3做)设计一个求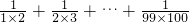 的值的程序框图.
的值的程序框图.查看答案和解析>>
科目:高中数学 来源:2009-2010学年湖南省永州市高一(上)期末数学试卷(解析版) 题型:解答题
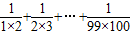 的值的程序框图.
的值的程序框图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com