Question

如图,等腰直角三角形ABC的斜边AB在x轴上,原点O为AB的中点,|AB|=4,D是OC的中点.以A、B为焦点的椭圆E经过点D.

(1)求椭圆E的方程;

(2)过点C的直线l与椭圆E相交于不同的两点M、N,点M在点C、N之间,且CM=λCN,求实数λ的取值范围.

Answer 1

解:(1)在等腰直角三角形ABC中,因为斜边|AB|=4,

所以|OA|=|OB|=|OC|=2.

所以椭圆的半焦距c=2.

因为D是OC的中点,所以椭圆的短半轴长b=1,

所以椭圆的长半轴长a=.

所以椭圆E的方程为+y²=1.

(2)设M(x₁,y₁),N(x₂,y₂),则=(x₁,y₁-2),=(x₂,y₂-2).

由=λ,得(x₁,y₁-2)=λ(x₂,y₂-2).

所以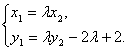                         ①

因为点M、N都在椭圆+y²=1上,

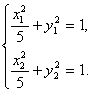所以                              ②

将①代入②得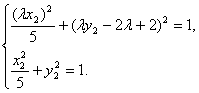

消去x₂,得(λy₂-2λ+2)²-λ²y₂²=1-λ².

所以y₂=.

根据题意,得-1≤y₂≤1,

所以-1≤≤1.

解得≤λ≤3.                                  ③

因为点M在点C、N之间,且=λ,

所以0＜λ＜1.                                 ④

根据③④,得≤λ＜1.