
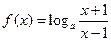 ,
,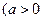 ,且
,且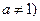
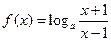 在定义域上是奇函数;
在定义域上是奇函数;
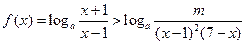 恒成立,求
恒成立,求 的取值范围;
的取值范围;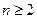 ,且
,且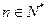 时,试比较
时,试比较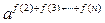 与
与 的大小.
的大小.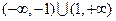 ,证明略
,证明略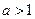 时,
时,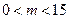 ;②当
;②当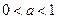 时,
时,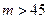
 时,
时,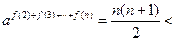

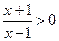 ,解得
,解得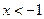 或
或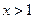 ,
,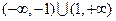 …………………2分
…………………2分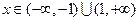 时,
时,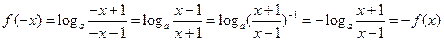
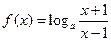 在定义域上是奇函数。 …………….4分
在定义域上是奇函数。 …………….4分 时,
时,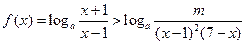 恒成立,
恒成立,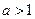 时
时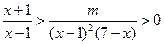 对
对 恒成立
恒成立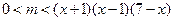 在
在 恒成立 ………………………6分
恒成立 ………………………6分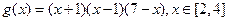
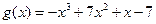
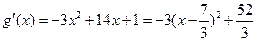
 时,
时,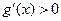
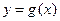 在区间
在区间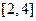 上是增函数,
上是增函数,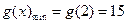
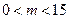 …………………………8分
…………………………8分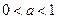 时
时 时,
时,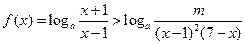 恒成立,
恒成立,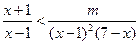 对
对 恒成立
恒成立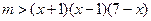 在
在 恒成立 ………………………9分
恒成立 ………………………9分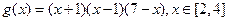
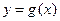 在区间
在区间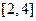 上是增函数,
上是增函数,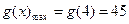
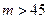 …………………………10分
…………………………10分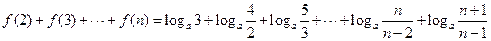
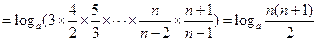
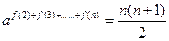
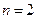 时,
时,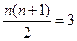 ,
, =2,∴
=2,∴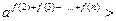

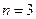 时,
时,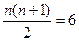 ,
, =6,∴
=6,∴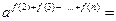

 时,
时,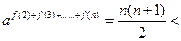
 …………………………12分
…………………………12分 时,
时,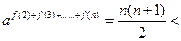

 时,
时,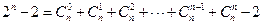
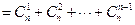
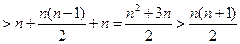
 时,
时,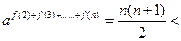
 …………………………14分
…………………………14分 时,要证明
时,要证明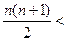

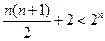
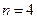 时,
时,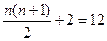 ,
,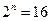 ,
,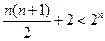 成立
成立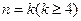 ,不等式
,不等式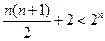 成立,即
成立,即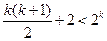
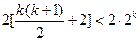
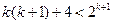
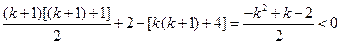
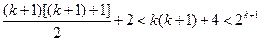
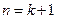 时,不等式
时,不等式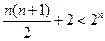 成立
成立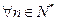 ,且
,且 不等式
不等式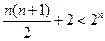 成立
成立 时,
时,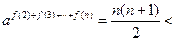
 …………………………14分
…………………………14分 时,
时,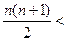

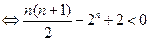
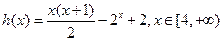
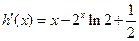
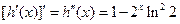
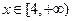 时,
时,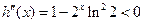
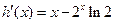 在区间
在区间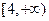 是减函数,
是减函数,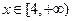 时,
时,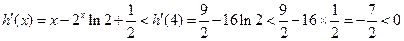
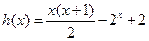 在区间
在区间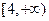 是减函数,
是减函数,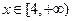 时,
时,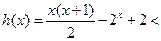

 时,
时,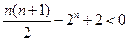 ,即
,即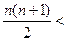

 时,
时,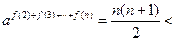
 …………………………14分
…………………………14分

科目:高中数学 来源:不详 题型:解答题
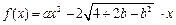 ,
,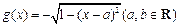 .
.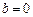 时,若
时,若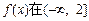 上单调递减,求a的取值范围;
上单调递减,求a的取值范围;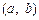 :存在
:存在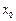 ,使得
,使得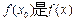 的最大值,
的最大值,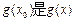 的最小值;
的最小值;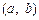 ,试构造一个定义在
,试构造一个定义在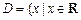 且
且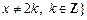 上的函数
上的函数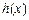 :使
:使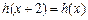 ,且当
,且当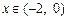 时,
时,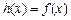 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
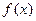 的图像恰好通过
的图像恰好通过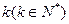 个格点,则称函数
个格点,则称函数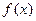 为k阶格点函数,下列函数中“一阶格点”函数有
为k阶格点函数,下列函数中“一阶格点”函数有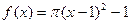 ②
②
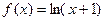 ④
④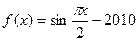
| A.②③ | B.①③ | C.①④ | D.②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com