已知i,m,n是正整数,且1<i≤m<n.
(1)证明niPmi<miPni;
(2)证明(1+m)n>(1+n)m.
【答案】
分析:(1)先将要证的不等式变形为分别含m,n的式子,再利用排列数公式,据不等式的性质得证
(2)利用二项式定理再利用(1)的结论和排列数和组合数的关系得证.
解答:证明:(1)对于1<i≤m有p
mi=m••(m-i+1),
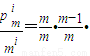

,
同理
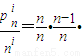
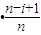
,
由于m<n,对整数k=1,2,i-1,有
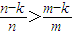
,
所以
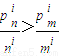
,即m
ip
ni>n
ip
mi.
(2)由二项式定理有

,

,
由(1)知m
ip
ni>n
ip
mi(1<i≤m<n),
而

,
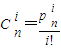
,
所以,m
iC
ni>n
iC
mi(1<i≤m<n).
因此,

.
又m
C
n=n
C
m=1,mC
n1=nC
m1=mn,m
iC
ni>0(1<i≤m<n).
∴

.
即(1+m)
n>(1+n)
m.
点评:本小题考查排列、组合、二项式定理、不等式的基本知识和逻辑推理能力.

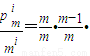
 ,
,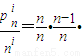
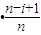 ,
,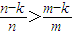 ,
,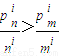 ,即mipni>nipmi.
,即mipni>nipmi. ,
, ,
, ,
,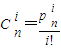 ,
, .
. .
.

 期末集结号系列答案
期末集结号系列答案