
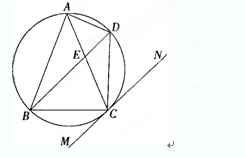
如图,△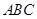 内接于⊙
内接于⊙ ,
,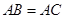 ,直线
,直线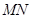 切⊙
切⊙ 于点
于点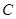 ,弦
,弦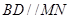 ,
,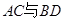 相交于点
相交于点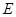 .
.
(Ⅰ)求证:△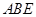 ≌△
≌△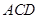 ;
;
(Ⅱ)若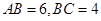 ,求
,求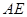 长.
长.
科目:高中数学 来源: 题型:解答题
如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.求证:
(1)∠AED=∠AFD;
(2)AB2=BE·BD-AE·AC.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD,求证: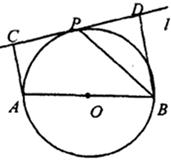
(1)l是⊙O的切线;
(2)PB平分∠ABD.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,设AB,CD为⊙O的两直径,过B作PB垂直于AB,并与CD延长线相交于点P,过P作直线与⊙O分别交于E,F两点,连结AE,AF分别与CD交于G、H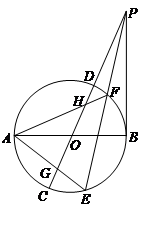
(Ⅰ)设EF中点为 ,求证:O、
,求证:O、 、B、P四点共圆
、B、P四点共圆
(Ⅱ)求证:OG =OH.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,过圆O外一点P作该圆的两条割线PAB和PCD,分别交圆 O于点A,B,C,D弦AD和BC交于Q点,割线PEF经过Q点交圆 O于点E、F,点M在EF上,且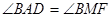 :
:
(I)求证:PA·PB=PM·PQ; (II)求证: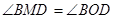 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com