
| 4200-x2 |
| 4500 |
| 4200-x2 |
| 4500 |
| 4200-x2 |
| 4500 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |


科目:高中数学 来源: 题型:
| 4200-x2 | 4500 |
查看答案和解析>>
科目:高中数学 来源: 题型:
某工厂每天生产某种产品最多不超过40件,并且在生产过程中产品的正品率P与每日生产产品件数x(x∈N*)间的关系为![]() ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%)
,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%)
(Ⅰ)将日利润y(元)表示成日产量x(件)的函数;
(Ⅱ)求该厂的日产量为多少件时,日利润最大?并求出日利润的最大值
查看答案和解析>>
科目:高中数学 来源:2014届辽宁省丹东市高二上学期期末考试文数试卷(解析版) 题型:解答题
(本小题满分12分) 某工厂每天生产某种产品最多不超过40件,并且在生产过程中产品的正品率P与每日生产产品件数x(x∈N*)间的关系为P= ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%).
,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%).
(Ⅰ)将日利润y(元)表示成日产量x(件)的函数;
(Ⅱ)求该厂的日产量为多少件时,日利润最大?并求出日利润的最大值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省仙桃市高三上学期第三次考试文科数学试卷(解析版) 题型:解答题
某工厂每天生产某种产品最多不超过40件,并且在生产过程中产品的正品率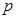 与每日生产产品件数
与每日生产产品件数 (
(
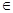
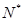 )间的关系为
)间的关系为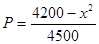 ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.
,每生产一件正品盈利4000元,每出现一件次品亏损2000元.
(注:正品率=产品的正品件数÷产品总件数×100%)
(1)将日利润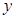 (元)表示成日产量
(元)表示成日产量 (件)的函数;
(件)的函数;
(2)求该厂的日产量为多少件时,日利润最大?并求出日利润的最大值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三10月阶段性测试文科数学试卷 题型:解答题
(14分)某工厂每天生产某种产品最多不超过40件,并且在生产过程中产品的正品率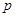 与每日生产产品件数
与每日生产产品件数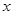 (
(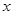

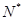 )间的关系为
)间的关系为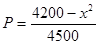 ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%)
,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%)
(Ⅰ)将日利润 (元)表示成日产量
(元)表示成日产量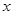 (件)的函数;
(件)的函数;
(Ⅱ)求该厂的日产量为多少件时,日利润最大?并求出日利润的最大值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com