

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源:2014届江西省红色六校高三第一次联考理科数学试卷(解析版) 题型:选择题
一电子广告,背景是由固定的一系列下顶点相接的正三角形组成,这列正三解形的底边在同一直线上,正三角形的内切圆由第一个正三角形的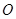 点沿三角形列的底边匀速向前滚动(如图),设滚动中的圆与系列正三角形的重叠部分(如图中的阴影)的面积
点沿三角形列的底边匀速向前滚动(如图),设滚动中的圆与系列正三角形的重叠部分(如图中的阴影)的面积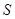 关于时间
关于时间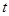 的函数为
的函数为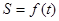 ,则下列图中与函数
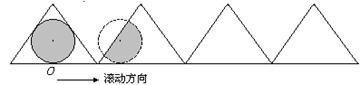
,则下列图中与函数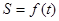 图像最近似的是( ).
图像最近似的是( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com