
【题目】已知四棱锥![]() 中,底面ABCD是梯形,且
中,底面ABCD是梯形,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,AD的中点为E,则四棱锥
,AD的中点为E,则四棱锥![]() 外接球的表面积为________.
外接球的表面积为________.
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知A,B是椭圆C:![]() )的左右顶点,P点为椭圆C上一点,点P关于x轴的对称点为H,且
)的左右顶点,P点为椭圆C上一点,点P关于x轴的对称点为H,且![]()
(1)若椭圆C经过了圆![]() 的圆心,求椭圆C的标准方程;
的圆心,求椭圆C的标准方程;
(2)在(1)的条件下,抛物线D:![]() 的焦点F与点
的焦点F与点![]() 关于y轴上某点对称,且抛物线D与椭圆C在第四象限交于点Q,过点Q作直线与抛物线D有唯一公共点,求该直线与两坐标轴围成的三角形面积.
关于y轴上某点对称,且抛物线D与椭圆C在第四象限交于点Q,过点Q作直线与抛物线D有唯一公共点,求该直线与两坐标轴围成的三角形面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在中美组织的暑假中学生交流会结束时,中方组织者将孙悟空、猪八戒、沙和尚、唐三藏、白龙马的彩色陶俑各一个送给来中国参观的美国中学生汤姆、杰克、索菲娅,每个人至少一个,且猪八戒的彩色陶俑不能送给索菲娅,则不同的送法种数为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,(其中
,(其中![]() )的图象关于点
)的图象关于点![]() 成中心对称,且与点
成中心对称,且与点![]() 相邻的一个最低点为
相邻的一个最低点为![]() ,则对于下列判断:
,则对于下列判断:
①直线![]() 是函数
是函数![]() 图象的一条对称轴;
图象的一条对称轴;
②点![]() 是函数
是函数![]() 的一个对称中心;
的一个对称中心;
③函数![]() 与
与![]() 的图象的所有交点的横坐标之和为
的图象的所有交点的横坐标之和为![]() .
.
其中所有正确的判断是( )
A.①②B.①③C.②③D.②
查看答案和解析>>
科目:高中数学 来源: 题型:
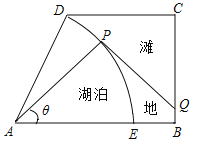
【题目】如图,某湿地公园的鸟瞰图是一个直角梯形,其中:![]() ,
,![]() ,
,![]() ,
,![]() 长1千米,
长1千米,![]() 长
长![]() 千米,公园内有一个形状是扇形的天然湖泊
千米,公园内有一个形状是扇形的天然湖泊![]() ,扇形
,扇形![]() 以
以![]() 长为半径,弧
长为半径,弧![]() 为湖岸,其余部分为滩地,B,D点是公园的进出口.公园管理方计划在进出口之间建造一条观光步行道:线段
为湖岸,其余部分为滩地,B,D点是公园的进出口.公园管理方计划在进出口之间建造一条观光步行道:线段![]() 线段
线段![]() 弧
弧![]() ,其中Q在线段
,其中Q在线段![]() 上(异于线段端点),
上(异于线段端点),![]() 与弧
与弧![]() 相切于P点(异于弧端点]根据市场行情
相切于P点(异于弧端点]根据市场行情![]() ,
,![]() 段的建造费用是每千米10万元,湖岸段弧
段的建造费用是每千米10万元,湖岸段弧![]() 的建造费用是每千米
的建造费用是每千米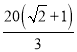 万元(步行道的宽度不计),设
万元(步行道的宽度不计),设![]() 为
为![]() 弧度观光步行道的建造费用为
弧度观光步行道的建造费用为![]() 万元.
万元.
(1)求步行道的建造费用![]() 关于
关于![]() 的函数关系式,并求其走义域;
的函数关系式,并求其走义域;
(2)当![]() 为何值时,步行道的建造费用最低?
为何值时,步行道的建造费用最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:![]() 与曲线C:
与曲线C:![]() (
(![]() ,
,![]() )交于不同的两点A,B,O为坐标原点.
)交于不同的两点A,B,O为坐标原点.
(1)若![]() ,
,![]() ,求证:曲线C是一个圆;
,求证:曲线C是一个圆;
(2)若曲线C过![]() 、
、![]() ,是否存在一定点Q,使得
,是否存在一定点Q,使得![]() 为定值?若存在,求出定点Q和定值;若不存在,请说明理由.
为定值?若存在,求出定点Q和定值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了了解高一年级学生学习数学的状态,从期中考试成绩中随机抽取50名学生的数学成绩,按成绩分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
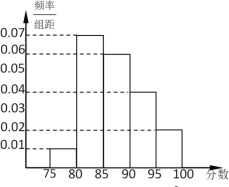
(1)由频率分布直方图,估计这50名学生数学成绩的中位数和平均数(保留到0.01);
(2)该校高一年级共有1000名学生,若本次考试成绩90分以上(含90分)为“优秀”等次,则根据频率分布直方图估计该校高一学生数学成绩达到“优秀”等次的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com