
【题目】定义在R上的奇函数f(x),对于x∈R,都有 ![]() ,且满足f(4)>﹣2,
,且满足f(4)>﹣2, ![]() ,则实数m的取值范围是 .
,则实数m的取值范围是 .
【答案】{mm<﹣1,或0<m<3}
【解析】解:∵ ![]() ; 用
; 用 ![]() 代换x得:
代换x得: ![]() ;
;
用 ![]() 代换x得:
代换x得: ![]() ;
;
即f(x)=f(x+3);
∴函数f(x)是以3为周期的周期函数;
∴f(4)=f(1)>﹣2,f(2)=﹣f(﹣2)=﹣f(﹣2+3)=﹣f(1)<2;
∴ ![]() ;
;
解得m<﹣1,或0<m<3;
∴实数m的取值范围为{m|m<﹣1,或0<m<3}.
所以答案是:{m|m<﹣1,或0<m<3}.
【考点精析】关于本题考查的函数奇偶性的性质,需要了解在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能得出正确答案.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}是公差不为零的等差数列,a10=15,且a3、a4、a7成等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某百货公司1~6月份的销售量x与利润y的统计数据如表:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售量x(万件) | 10 | 11 | 13 | 12 | 8 | 6 |
利润y(万元) | 22 | 25 | 29 | 26 | 16 | 12 |
(参考公式: ![]() =
= 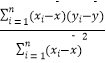 )=
)= 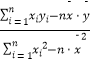 ,
, ![]() .
.
(1)根据2~5月份的统计数据,求出y关于x的回归直线方程 ![]() ;
;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差均不超过2万元,则认为得到的回归直线方程是理想的,试问所得回归直线方程是否理想?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)对任意实数x,y均有f(x)=f( ![]() )+f(
)+f( ![]() ).当x>0时,f(x)>0
).当x>0时,f(x)>0
(1)判断函数f(x)在R上的单调性并证明;
(2)设函数g(x)与函数f(x)的奇偶性相同,当x≥0时,g(x)=|x﹣m|﹣m(m>0),若对任意x∈R,不等式g(x﹣1)≤g(x)恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)= ![]() ﹣
﹣ ![]() ,若规定<x>表示不小于x的最小整数,则函数y=<f(x)>的值域是( )
,若规定<x>表示不小于x的最小整数,则函数y=<f(x)>的值域是( )
A.{0,1}
B.{0,﹣1}
C.{﹣1,1}
D.{﹣1,0,1}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为2的正方体内有一四面体A﹣BCD,其中B,C分别为正方体两条棱的中点,其三视图如图所示,则四面体A﹣BCD的体积为( ) 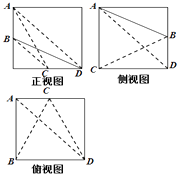
A.![]()
B.2
C.![]()
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com