(1)解:∵PF
1⊥x轴,∴F
1(-1,0),c=1,F
2(1,0),
∴|PF
2|=
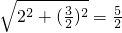
,∴2a=|PF
1|+|PF
2|=4,∴a=2,∴b
2=3,
∴椭圆E的方程为:

;…(3分)
(2)证明:设A(x
1,y
1)、B(x
2,y
2),
由
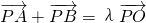
得(x
1+1,y
1-

)+(x
2+1,y
2-

)=λ(1,-

),
所以x
1+x
2=λ-2,y
1+y
2=

(2-λ)…①…(5分)
又
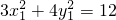
,

,
两式相减得3(x
1+x
2)(x
1-x
2)+4(y
1+y
2)(y
1-y
2)=0…..②
以①式代入可得AB的斜率k=
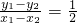
=

=e;…(8分)
(3)解:设直线AB的方程为y=

x+t,与3x
2+4y
2=12联立消去y并整理得 x
2+tx+t
2-3=0,△=3(4-t
2),
|AB|=

,
点P到直线AB的距离为d=

,
△PAB的面积为S=

|AB|×d=
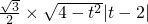
,…(10分)
设f(t)=S
2=

(t
4-4t
3+16t-16)(-2<t<2),
f′(t)=-3(t
3-3t
2+4)=-3(t+1)(t-2)
2,由f′(t)=0及-2<t<2得t=-1.
当t∈(-2,-1)时,f′(t)>0,当t∈(-1,2)时,f′(t)<0,f(t)=-1时取得最大值

,
所以S的最大值为

.
此时x
1+x
2=-t=1=λ-2,λ=3.…(12分)
分析:(1)求出|PF
1|、|PF
2|,利用椭圆的定义,即可求得椭圆E的方程;
(2)利用
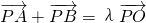
确定坐标之间的关系,点的坐标代入方程,利用点差法,即可证得结论;
(3)设直线AB的方程与3x
2+4y
2=12联立消去y并整理,求出|AB|、点P到直线AB的距离,从而可得△PAB的面积利用导数法求最大值,即可得到结论.
点评:本题考查椭圆的标准方程,考查向量知识的运用,考查点差法,考查直线与椭圆的位置关系,考查导数知识的运用,确定三角形的面积是关键.

 )是椭圆E:
)是椭圆E: (a>b>0)上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.
(a>b>0)上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.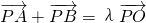 (0<λ<4,且λ≠2).求证:直线AB的斜率等于椭圆E的离心率;
(0<λ<4,且λ≠2).求证:直线AB的斜率等于椭圆E的离心率;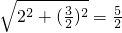 ,∴2a=|PF1|+|PF2|=4,∴a=2,∴b2=3,
,∴2a=|PF1|+|PF2|=4,∴a=2,∴b2=3, ;…(3分)
;…(3分)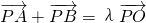 得(x1+1,y1-
得(x1+1,y1- )+(x2+1,y2-
)+(x2+1,y2- )=λ(1,-
)=λ(1,- ),
), (2-λ)…①…(5分)
(2-λ)…①…(5分)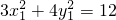 ,
, ,
,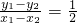 =
= =e;…(8分)
=e;…(8分) x+t,与3x2+4y2=12联立消去y并整理得 x2+tx+t2-3=0,△=3(4-t2),
x+t,与3x2+4y2=12联立消去y并整理得 x2+tx+t2-3=0,△=3(4-t2), ,
, ,
, |AB|×d=
|AB|×d=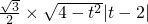 ,…(10分)
,…(10分) (t4-4t3+16t-16)(-2<t<2),
(t4-4t3+16t-16)(-2<t<2), ,
, .
.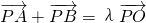 确定坐标之间的关系,点的坐标代入方程,利用点差法,即可证得结论;
确定坐标之间的关系,点的坐标代入方程,利用点差法,即可证得结论;

 名校课堂系列答案
名校课堂系列答案 )是曲线f(x)=Asin(ωx+φ)(A>0,ω>0|φ|<
)是曲线f(x)=Asin(ωx+φ)(A>0,ω>0|φ|< )的一个最高点,且f(9-x)=f(9+x),曲线区间(1,9)内与x轴有唯一一个交点,求这个函数的解析式,并作出一个周期的图象.
)的一个最高点,且f(9-x)=f(9+x),曲线区间(1,9)内与x轴有唯一一个交点,求这个函数的解析式,并作出一个周期的图象. )是椭圆E:
)是椭圆E: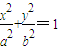 (a>b>0)上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.
(a>b>0)上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.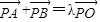 (0<λ<4,且λ≠2).求证:直线AB的斜率等于椭圆E的离心率;
(0<λ<4,且λ≠2).求证:直线AB的斜率等于椭圆E的离心率;