
分析 根据条件可以得出$\frac{ac}{{b}^{2}}≥\frac{1}{4}$,且a,c>0,而$\frac{f(1)}{b}=\frac{a}{b}+\frac{c}{b}+1$,这样根据基本不等式以及不等式的性质即可得出$\frac{f(1)}{b}$的最小值.
解答 解:根据条件知,△=b2-4ac≤0,且a>0;
∴b2≤4ac;
$\frac{ac}{{b}^{2}}≥\frac{1}{4}$;
∴c>0,又b>0;
∴$\frac{f(1)}{b}=\frac{a+b+c}{b}=\frac{a}{b}+\frac{c}{b}+1≥2\sqrt{\frac{ac}{{b}^{2}}}+1$$≥2\sqrt{\frac{1}{4}}+1=2$;
∴$\frac{f(1)}{b}$的最小值为2.
故答案为:2.
点评 考查当二次函数f(x)=ax2+bx+c恒大于0时,便可得到△≤0,a>0,不等式的性质,以及基本不等式的运用,注意应用基本不等式所要具备的条件.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y={x^{\frac{3}{2}}}$ | B. | $y={x^{\frac{2}{3}}}$ | C. | $y={x^{-\frac{1}{3}}}$ | D. | $y={x^{\frac{1}{3}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
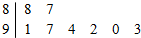 某市8所中学生参加比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
某市8所中学生参加比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )| A. | 91 5.5 | B. | 91 5 | C. | 92 5.5 | D. | 92 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com