
分析 设直线PA与平面α所成的角为θ,则sinθ=|cosα|=$\frac{|\overrightarrow{n}•\overrightarrow{PA}|}{|\overline{n}||\overrightarrow{PA}|}$,即可得出.
解答 解:设直线PA与平面α所成的角为θ,则sinθ=|cosα|=$\frac{|\overrightarrow{n}•\overrightarrow{PA}|}{|\overline{n}||\overrightarrow{PA}|}$=$\frac{|0-\frac{1}{4}-2|}{\sqrt{0+\frac{1}{4}+2}\sqrt{\frac{3}{4}+\frac{1}{4}+2}}$=$\frac{\sqrt{3}}{2}$,
∴直线PA与平面α所成的角为$\frac{π}{3}$.
故答案为:$\frac{π}{3}$.
点评 本题考查了线面角的计算公式、数量积运算性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | R | B. | {0} | C. | {x|x∈R,x≠0} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{5}$i | B. | -$\frac{1}{5}$ | C. | $\frac{1}{5}$i | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
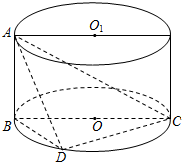 如图所示,圆柱O1O中,母线AB与底面垂直,BC是⊙O的直径,点D是⊙O的圆周上异于B,C的点.
如图所示,圆柱O1O中,母线AB与底面垂直,BC是⊙O的直径,点D是⊙O的圆周上异于B,C的点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | 2 | C. | 3 | D. | $\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com