
A.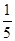 | B.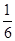 | C.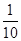 | D.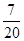 |
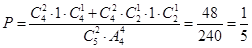 , 故选A.
, 故选A. 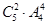 是所有可能情况,即5个人里面选2个人做一堆即
是所有可能情况,即5个人里面选2个人做一堆即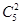 ,然后将剩余的3人和选好的两人共4堆做全排列即
,然后将剩余的3人和选好的两人共4堆做全排列即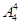 对应于4台电脑的位置,所以是
对应于4台电脑的位置,所以是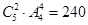
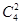 种,剩下的两台电脑和两名同学的配对关系则是固定的,即有
种,剩下的两台电脑和两名同学的配对关系则是固定的,即有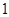 种,然后是给5号同学选择电脑
种,然后是给5号同学选择电脑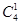 种,所以是
种,所以是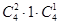 种.
种.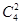 种,在剩下的两台电脑里面选择一台给5号同学单独使用,即有
种,在剩下的两台电脑里面选择一台给5号同学单独使用,即有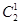 种,则最后一台电脑的使用者是固定的,再将最后一位同学放入先前编号与使用者编号相同的两台电脑中,即有
种,则最后一台电脑的使用者是固定的,再将最后一位同学放入先前编号与使用者编号相同的两台电脑中,即有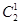 种,所以是
种,所以是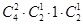 种.
种.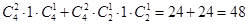 种.
种.

科目:高中数学 来源:不详 题型:单选题
| A.至少有一个红球与都是红球 |
| B.至少有一个红球与都是白球 |
| C.至少有一个红球与至少有一个白球 |
| D.恰有一个红球与恰有二个红球 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.1/1000 | B.1/100 | C.1/10 | D.1/9 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
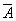 是A的对立事件,
是A的对立事件,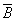 是B的对立事件。若和事件A+B发生的概率为0.4,则积事件
是B的对立事件。若和事件A+B发生的概率为0.4,则积事件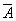 ·
·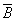 发生的概率为( )
发生的概率为( )| A.0.24 | B.0.36 | C.0.4 | D.0.6 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
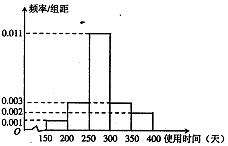
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com