
【题目】已知函数![]() ,
,![]() .
.
(l)设![]() ,讨论函数
,讨论函数![]() 的单调性;
的单调性;
(2)若函数![]() 的图象在
的图象在![]() 上恒在
上恒在![]() 轴的上方,求实数
轴的上方,求实数![]() 的取值范围.
的取值范围.
【答案】(1)详见解析;(2)![]()
【解析】
(1)先求导函数![]() ,然后通过对
,然后通过对![]() 和
和![]() 讨论,判断导函数的正负,从而可求出函数的单调区间;
讨论,判断导函数的正负,从而可求出函数的单调区间;
(2)“若函数![]() 的图象在
的图象在![]() 上恒在
上恒在![]() 轴的上方”等价于“不等式
轴的上方”等价于“不等式![]() 在
在![]() 上恒成立”, 即不等式
上恒成立”, 即不等式![]() 在
在![]() 上恒成立,即不等式可转化为
上恒成立,即不等式可转化为![]() 在
在![]() 上恒成立,然后构造函数
上恒成立,然后构造函数![]() ,只需
,只需![]() 在
在![]() 上最大值小于零即可,从而可求出
上最大值小于零即可,从而可求出![]() 的取值范围.
的取值范围.
(1)![]() ,
,![]() ,
,
![]() .
.
①若![]() ,
,![]() ,
,![]() ,函数
,函数![]() 的单调减区间是
的单调减区间是![]() ,无单调增区间;
,无单调增区间;
②若![]() ,令
,令![]() ,得
,得![]() ;
;
令![]() ,得
,得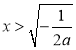 ,
,
所以函数![]() 的单调减区间是
的单调减区间是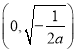 ,单调增区间是
,单调增区间是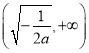 .
.
综上所述,若![]() ,函数
,函数![]() 的单调减区间是
的单调减区间是![]() ,无单调增区间;
,无单调增区间;
若![]() ,函数
,函数![]() 的单调减区间是
的单调减区间是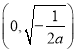 ,单调增区间是
,单调增区间是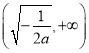 .
.
(2)“若函数![]() 的图象在
的图象在![]() 上恒在
上恒在![]() 轴的上方”等价于“不等式
轴的上方”等价于“不等式![]() 在
在![]() 上恒成立”,
上恒成立”,
即不等式![]() 在
在![]() 上恒成立,
上恒成立,
即不等式可转化为![]() 在
在![]() 上恒成立.
上恒成立.
令![]() ,
,
则![]()
![]() .
.
①若![]() ,则
,则![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,不等式恒成立等价于
,不等式恒成立等价于![]() ,即
,即![]() ;
;
②若![]() ,则
,则![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() ,不符合题意;
,不符合题意;
③若![]() ,当
,当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,不符合题意.
,不符合题意.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
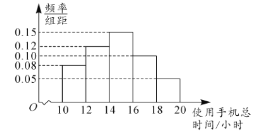
【题目】为了解学生课外使用手机的情况,某学校收集了本校500名学生2019年12月课余使用手机的总时间(单位:小时)的情况.从中随机抽取了50名学生,将数据进行整理,得到如图所示的频率分布直方图.已知这50名学生中,恰有3名女生课余使用手机的总时间在![]() ,现在从课余使用手机总时间在
,现在从课余使用手机总时间在![]() 的样本对应的学生中随机抽取3名,则至少抽到2名女生的概率为( )
的样本对应的学生中随机抽取3名,则至少抽到2名女生的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】维生素C又叫抗坏血酸,是一种水溶性维生素,是高等灵长类动物与其他少数生物的必需营养素.维生素C虽不直接构成脑组织,也不向脑提供活动能源,但维生素C有多种健脑强身的功效,它是脑功能极为重要的营养物.维生素C的毒性很小,但食用过多仍可产生一些不良反应.根据食物中维C的含量可大致分为:含量很丰富:鲜枣、沙棘、猕猴桃、柚子,每100克中的维生素C含量超过100毫克;比较丰富:青椒、桂圆、番茄、草莓、甘蓝、黄瓜、柑橘、菜花,每100克中维生素C含量超过50毫克;相对丰富:白菜、油菜、香菜、菠菜、芹菜、苋菜、菜苔、豌豆、豇豆、萝卜,每100克中维生素C含量超过30~50毫克.现从猕猴桃、柚子两种食物中测得每100克所含维生素C的量(单位:![]() )得到茎叶图如图所示,则下列说法中不正确的是( )
)得到茎叶图如图所示,则下列说法中不正确的是( )
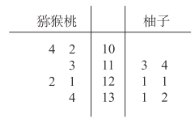
A.猕猴桃的平均数小于柚子的平均数
B.猕猴桃的方差小于柚子的方差
C.猕猴桃的极差为32
D.柚子的中位数为121
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,
,![]() ,三角形
,三角形![]() 是边长为2的正三角形,当四棱锥
是边长为2的正三角形,当四棱锥![]() 的外接球的体积取得最小值时,则以下判断正确的是( )
的外接球的体积取得最小值时,则以下判断正确的是( )
A.四棱锥![]() 的体积取得最小值为
的体积取得最小值为![]() ,外接球的球心必在四棱锥
,外接球的球心必在四棱锥![]() 内
内
B.四棱锥![]() 的体积取得最小值为
的体积取得最小值为![]() ,外接球的球心可在四棱锥
,外接球的球心可在四棱锥![]() 内或外
内或外
C.四棱锥![]() 的体积为
的体积为![]() ,外接球的球心必在四棱锥
,外接球的球心必在四棱锥![]() 内
内
D.四棱锥![]() 的体积为
的体积为![]() ,外接球的球心可在四棱锥
,外接球的球心可在四棱锥![]() 内或外
内或外
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 已知函数f(x)=|x+a|+|x-2|.
(1)当a=-3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com