
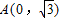 和圆O1:
和圆O1: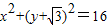 ,点M在圆O1上运动,点P在半径O1M上,且|PM|=|PA|,求动点P的轨迹方程.
,点M在圆O1上运动,点P在半径O1M上,且|PM|=|PA|,求动点P的轨迹方程.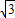 ),O1(0,
),O1(0,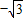 )为焦点的椭圆.根据椭圆的基本概念求出椭圆方程,即可得到动点P的轨迹方程.
)为焦点的椭圆.根据椭圆的基本概念求出椭圆方程,即可得到动点P的轨迹方程.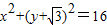 是以O1(0,-
是以O1(0,-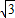 )为圆心,半径r=4的圆
)为圆心,半径r=4的圆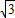 ),O1(0,
),O1(0,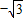 )的距离之和为4(常数)
)的距离之和为4(常数)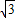 ),O1(0,
),O1(0,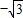 )为焦点的椭圆,
)为焦点的椭圆,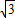 且2a=4,
且2a=4,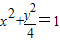
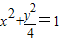 .
.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:辽宁省大连市2012届高三双基测试数学理科试题 题型:044
如图所示,已知⊙O1和⊙O2相交于A、B两点,过A点作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1、⊙O2于点D、E,DE与AC相交于点P.
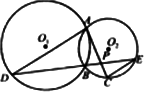
(Ⅰ)求证:AD∥EC;
(Ⅱ)若AD是⊙O2的切线,且PA=6,PC=2,BD=9,求AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
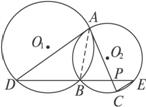
图2-5-11
(1)求证:AD∥EC;
(2)若AD是⊙O2的切线,且PA=6,PC=2,BD=9,求AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求动圆圆心P的轨迹C的方程,并说明轨迹C是什么曲线.
(2)已知点A(-6,0),O2(3,0).当点M在曲线C上运动时,求F(M)=3![]() ·
·![]() ?+2
?+2![]() ·
·![]() +
+![]() ·
·![]() 的最大值和最小值,并指出取得最值时点M的坐标.
的最大值和最小值,并指出取得最值时点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com