
【题目】F1 , F2分别是双曲线 ![]() ﹣
﹣ ![]() =1(a,b>0)的左右焦点,点P在双曲线上,满足
=1(a,b>0)的左右焦点,点P在双曲线上,满足 ![]() =0,若△PF1F2的内切圆半径与外接圆半径之比为
=0,若△PF1F2的内切圆半径与外接圆半径之比为 ![]() ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )
A.![]()
B.![]()
C.![]() +1
+1
D.![]() +1
+1
【答案】D
【解析】解:设P为双曲线的右支上一点, ![]()
![]() =0,即为
=0,即为 ![]() ⊥
⊥ ![]() ,
,
由勾股定理可得|PF1|2+|PF2|2=|F1F2|2=4c2 , ①
由双曲线的定义可得|PF1|﹣|PF2|=2a,②
①﹣②2 , 可得|PF1||PF2|=2(c2﹣a2),
可得|PF1|+|PF2|= ![]() ,
,
由题意可得△PF1F2的外接圆的半径为 ![]() |F1F2|=c,
|F1F2|=c,
设△PF1F2的内切圆的半径为r,可得![]() |PF1||PF2|=
|PF1||PF2|= ![]() r(|PF1|+|PF2|+|F1F2|),
r(|PF1|+|PF2|+|F1F2|),
解得r= ![]() (
( ![]() ﹣2c),
﹣2c),
即有 ![]() =
= ![]() ,
,
化简可得8c2﹣4a2=(4+2 ![]() )c2 ,
)c2 ,
即有c2= ![]() a2 ,
a2 ,
则e= ![]() =
= ![]() =
= ![]() +1.
+1.
故选:D.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn , 且Sn=n(n+1)(n∈N*)
(1)求数列{an}的通项公式;
(2)若数列{bn}满足:an= ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;
(3)令cn= ![]() (n∈N*),求数列{cn}的前n项和Tn .
(n∈N*),求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明准备利用暑假时间去旅游,妈妈为小明提供四个景点,九寨沟、泰山、长白山、武夷山.小明决定用所学的数学知识制定一个方案来决定去哪个景点:(如图)曲线 ![]() 和直线
和直线 ![]() 交于点
交于点 ![]() .以
.以 ![]() 为起点,再从曲线
为起点,再从曲线 ![]() 上任取两个点分别为终点得到两个向量,记这两个向量的数量积为
上任取两个点分别为终点得到两个向量,记这两个向量的数量积为 ![]() .若
.若 ![]() 去九寨沟;若
去九寨沟;若 ![]() 去泰山;若
去泰山;若 ![]() 去长白山;
去长白山; ![]() 去武夷山.
去武夷山.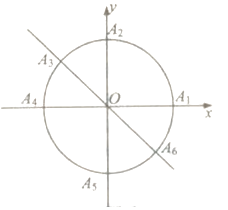
(1)若从 ![]() 这六个点中任取两个点分别为终点得到两个向量,分别求小明去九寨沟的概率和不去泰山的概率;
这六个点中任取两个点分别为终点得到两个向量,分别求小明去九寨沟的概率和不去泰山的概率;
(2)按上述方案,小明在曲线 ![]() 上取点
上取点 ![]() 作为向量的终点,则小明决定去武夷山.点
作为向量的终点,则小明决定去武夷山.点 ![]() 在曲线
在曲线 ![]() 上运动,若点
上运动,若点 ![]() 的坐标为
的坐标为 ![]() ,求
,求 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD-A1B1C1D1 , O是底面ABCD对角线的交点.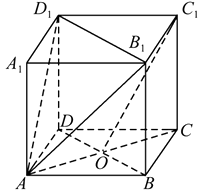
求证:(I) C1O∥面AB1D1;
(II)面A1C⊥面AB1D1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,四边形ACFE是矩形,且平面ACFE⊥平面ABCD,点M在线段EF上. (I)求证:BC⊥平面ACFE;
(II)当EM为何值时,AM∥平面BDF?证明你的结论.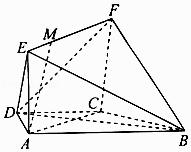
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(ωx+φ), ![]() 的最小正周期为π,且图象关于x=
的最小正周期为π,且图象关于x= ![]() 对称.
对称.
(1)求ω和φ的值;
(2)将函数f(x)的图象上所有横坐标伸长到原来的4倍,再向右平移 ![]() 个单位得到函数g(x)的图象,求g(x)的单调递增区间以及g(x)≥1的x取值范围.
个单位得到函数g(x)的图象,求g(x)的单调递增区间以及g(x)≥1的x取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若抛物线y2=2px上恒有关于直线x+y﹣1=0对称的两点A,B,则p的取值范围是( )
A.(﹣ ![]() ,0)
,0)
B.(0, ![]() )
)
C.(0, ![]() )
)
D.(﹣∞,0)∪( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 为偶函数.
为偶函数.
(1)求实数t值;
(2)记集合E={y|y=f(x),x∈{1,2,3}},λ=lg22+lg2lg5+lg5﹣1,判断λ与E的关系;
(3)当x∈[a,b](a>0,b>0)时,若函数f(x)的值域为[2﹣ ![]() ,2﹣
,2﹣ ![]() ],求实数a,b的值.
],求实数a,b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com