
【题目】如图所示的三棱台中,![]() 分别为
分别为![]() 的中点,
的中点,![]() ,
,![]() .
.
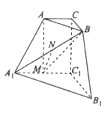
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
①命题“2是素数且5是素数”是真命题
②命题“若x=y,则sinx=siny”的逆命题是真命题
③命题“x0∈R,x02﹣x0﹣2>0”的否定是“x∈R,x2﹣x﹣2≤0”
A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与PM2.5的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与PM2.5的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量×(万辆) | 50 | 51 | 54 | 57 | 58 |
PM2.5的浓度(微克/立方米) | 60 | 70 | 74 | 78 | 79 |
(1)根据上表数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(2)若周六同一时间段的车流量是25万辆,试根据(1)求出的线性回归方程,预测此时PM2.5的浓度为多少(保留整数)?
参考公式:由最小二乘法所得回归直线的方程是:![]() ,其中
,其中 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·江苏高考)如图,在三棱锥ABCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.

求证:(1)EF∥平面ABC;
(2)AD⊥AC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x)若存在x0∈R,f(x0)=x0成立,则称x0为f(x)的不动点.已知f(x)=ax2+(b+1)x+b-1(a≠0).
(1)当a=1,b=-2时,求函数f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围;
(3)在(2)的条件下,若y=f(x)图象上A,B两点的横坐标是函数f(x)的不动点,且A,B两点关于直线y=kx+![]() 对称,求b的最小值.
对称,求b的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
11分制乒乓球比赛,每赢一球得1分,当某局打成10:10平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为0.5,乙发球时甲得分的概率为0.4,各球的结果相互独立.在某局双方10:10平后,甲先发球,两人又打了X个球该局比赛结束.
(1)求P(X=2);
(2)求事件“X=4且甲获胜”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com