
某车间加工零件的数量 与加工时间
与加工时间 的统计数据如下表:
的统计数据如下表:
零件数 (个) (个) | 10 | 20 | 30 |
加工时间 (分钟) (分钟) | 21 | 30 | 39 |
 中的
中的 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )科目:高中数学 来源: 题型:解答题
选修4—4:坐标系与参数方程
在极坐标系中,曲线 ,
,
过点A(5,α)(α为锐角且 )作平行于
)作平行于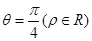 的直线
的直线 ,且
,且 与曲线L分别交于B,C两点。
与曲线L分别交于B,C两点。
(Ⅰ)以极点为原点,极轴为x轴的正半轴,取与极坐标相同单位长度,建立平面直角坐标系,写出曲线L和直线 的普通方程;
的普通方程;
(Ⅱ)求|BC|的长。
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
设某大学的女生体重 (单位:
(单位: )与身高
)与身高 (单位:
(单位: )具有线性相关关系,根据一组样本数据
)具有线性相关关系,根据一组样本数据 (
(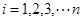 ),用最小二乘法建立的回归方程为
),用最小二乘法建立的回归方程为 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A. 与 与 具有正的线性相关关系 具有正的线性相关关系 |
B.回归直线过样本点的中心 |
C.若该大学某女生身高增加 ,则其体重约增加 ,则其体重约增加 |
D.若该大学某女生身高为 ,则可断定其体重为 ,则可断定其体重为 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知样本7,10,14,8,7,12,11,10,8,10,13,10,8,11,8,9,12,9,13,20,那么这组数据落在8.5~11.5的频率为( )
| A.0.5 | B.0.4 | C.0.3 | D.0.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知x、y的取值如下表所示:
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | 4.8 | m |
 ,则m的值为
,则m的值为 D、6.8
D、6.8查看答案和解析>>
科目:高中数学 来源: 题型:单选题
下表提供了某厂节能降耗技术改造后生产某产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨)的几组对应数据. 根据表中提供的数据,求出
(吨)的几组对应数据. 根据表中提供的数据,求出 关于
关于 的线性回归方程是
的线性回归方程是 ,那么表中
,那么表中 的值是( )
的值是( )
 | 3 | 4 | 5 | 6 |
 | 2.5 |  | 4 | 4.5 |
 B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
一个容量为20的样本,数据的分组及各组的频数如下:
(10,20 ,2;(20,30
,2;(20,30 ,3;(30,40
,3;(30,40 ,4;(40,50
,4;(40,50 ,5;(50,60
,5;(50,60 ,4;(60,70
,4;(60,70 ,2.
,2.
则样本在区间(10,50 上的频率为( )
上的频率为( )
| A.0.5 | B.0.7 | C.0.25 | D.0.05 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com