练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知为不同的直线，为不同的平面，给出下列四个命题：

    ①若，则；               ②若，则；

    ③若，则；   ④若，则.

    其中所有正确命题的序号是（    ）

             A．①②   B．②③           C．①③          D．①④

     

    【答案】

    D

    【解析】

    试题分析：由线面垂直的定义可知①正确；②中“”也有可能；③中必须“”；由面面垂直的性质定理可知④正确.故选答案D.

    考点：点、线、面的位置关系、定理.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知椭圆W的中心在原点，焦点在x轴上，离心率为
    		6
    3
    ，焦距为4，椭圆W的左焦点为F，过点M（-3，0）任作一条斜率不为零的直线l与椭圆W交于不同的两点A、B，点A关于x轴的对称点为C．
    （1）求椭圆W的方程；
    （2）
    CF
    =λ
    FB
    （λ∈R）是否成立？并说明理由；
    （3）求△MBC面积S的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知椭圆C：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0），直线y=x+
    		6
    与以原点为圆心，以椭圆C的短半轴长为半径的圆相切，F1、F2为其左、右焦点，P为椭圆C上任一点，△F1PF2的重心为G，内心为I，且IG∥F1F2．
    （1）求椭圆C的方程；
    （2）若直线l：y=kx+m（k≠0）与椭圆C交于不同的两点A、B，且线段AB的垂直平分线l′过定点Q（
    1
    6
    ，0），求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年福建省泉州市毕业班（第二轮）质量检测文科数学试卷（解析版） 题型：解答题

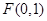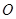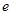    已知是中心在坐标原点的椭圆的一个焦点，且椭圆的离心率为．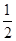

    （Ⅰ）求椭圆的方程；

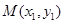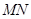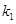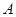    （Ⅱ）设：、为椭圆上不同的点，直线的斜率为；是满足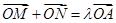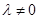（）的点，且直线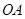的斜率为．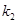

    ①求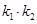的值；

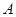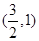    ②若的坐标为，求实数的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年辽宁省高三入学摸底考试文科数学试卷（解析版） 题型：选择题

    已知是不同的直线,是不同的平面,若①②③④,则其中能使的充分条件的个数为(    )

    A.0个           B.1个           C.2个           D.3个

     

    查看答案和解析>>

    同步练习册答案