已知数列{an}中,an=2n-33,求数列{|an|}的前n项和Sn.
解:令a
n=2n-33>0,解得n>
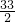
,
所以当n≤16时,a
n<0,又a
1=2-33=-31,
则数列{|a
n|}的前n项和S
n=-

=-
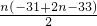
=32n-n
2;
当n≥17时,a
n>0,
则数列{|a
n|}的前n项和S
n=S
16+S
n-16=
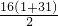
+
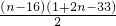
=n
2-32n+512,
综上,S
n=
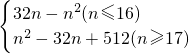
.
分析:令数列的通项公式大于0,解出n的取值范围,进而得到数列的前16项为负数,第17项开始为正数,所以分n小于等于16和n大于等于17两种情况,先根据数列的通项公式求出首项,利用等差数列的前n项和公式求出S
n,得到当n小于等于16时,-S
n为数列{|a
n|}的前n项和;当n大于等于17时,先求出前16项的和,再求出从第17项到第n项的和,两者相加即可得到数列{|a
n|}的前n项和.
点评:此题考查学生灵活运用等差数列的前n项和公式化简求值,是一道基础题.判断数列的项的正负是解本题的关键.

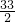 ,
, =-
=-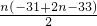 =32n-n2;
=32n-n2;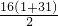 +
+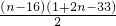 =n2-32n+512,
=n2-32n+512,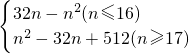 .
.
