分析:(1)根据图象可得到函数在x=0处的函数值与导数都等于0,就可求出c,d的值,再通过图象判断函数的单调性,得到导数取正值和负值的范围,因为导数是关于x的二次函数,根据导数何时取正值,何时取负值,就可判断a的符号,和对称轴的符号,进而得到b的范围.
(2)先由x
1=1,得f′(1)=0,从而f(x)=-
bx
3+bx
2,再构造新函数h(x))=f(x)-g(x)=-
bx
3+(b-e)x
2=x
2(-
bx+b-e),若在[0,e]上至少存在一点x
0,使得f(x
0)>g(x
0)成立,只需h(x)>0在[0,e]上有解,即-
bx+b-e>0在[0,e]上有解,最后将问题转化为求函数y=-
bx+b-e在[0,e]上的最大值问题即可
解答:解:(1)证明:
⇒f(x)=ax3+bx2=x2(ax+b)∴f′(x)=3ax
2+bx,通过图象可得出,
当x<0时,原函数为减函数,当0<x<x
1时,原函数为增函数,当x>x
1时,原函数为减函数,
∴当x<0时,导数小于0,当0<x<x
1时,导数大于0,当x>x
1时,导数小于0,
∴导函数f′(x)=3ax
2+bx图象为开口向下的抛物线,且对称轴在0和x
1之间
∴a<0,
->0,∴b>0
(2)解:∵f′(1)=0,∴b=-3a,∴f(x)=-
bx
3+bx
2
令h(x)=f(x)-g(x)=-
bx
3+(b-e)x
2=x
2(-
bx+b-e)
若在[0,e]上至少存在一点x
0,使得f(x
0)>g(x
0)成立
即h(x)>0在[0,e]上有解,即-
bx+b-e>0在[0,e]上有解
只需y=-
bx+b-e在[0,e]上的最大值大于零,
∵b>0
∴y=-
bx+b-e在[0,e]上的最大值为b-e
∴b>e即可
点评:本题考察了导数应用,转化化归的思想方法,解题时要透彻理解函数性质与方程、不等式的内在联系,准确解题

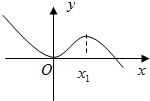 如图,函数f(x)=ax3+bx2+cx+d图象与x轴相切于原点.
如图,函数f(x)=ax3+bx2+cx+d图象与x轴相切于原点.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 已知如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象
已知如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象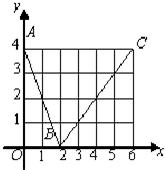 如图,函数f(x)的图象是折线段ABC,其中点A、B、C的坐标分别为(0,4),(2,0),(6,4),若f(x)的值域为[0,4],定义域为[m,n],则|m-n|的最小值为
如图,函数f(x)的图象是折线段ABC,其中点A、B、C的坐标分别为(0,4),(2,0),(6,4),若f(x)的值域为[0,4],定义域为[m,n],则|m-n|的最小值为