化简:$\frac{1}{2!}$+$\frac{2}{3!}$+$\frac{3}{4!}$+-+$\frac{n-1}{n!}$．(n∈N*.n≥2) 题目和参考答案——青夏教育精英家教网—

15．化简：$\frac{1}{2！}$+$\frac{2}{3！}$+$\frac{3}{4！}$+…+$\frac{n-1}{n!}$．（n∈N^*，n≥2）

分析原式利用题中的新定义变形，找出规律，以此类推得到结果即可．

解答解：$\frac{1}{2！}$+$\frac{2}{3！}$+$\frac{3}{4！}$+…+$\frac{n-1}{n!}$
=$\frac{2！-1}{2！}$+$\frac{2}{3！}$+$\frac{3}{4！}$+…+$\frac{n-1}{n!}$
=1-$\frac{1}{2！}$+$\frac{2}{3！}$+$\frac{3}{4！}$+…+$\frac{n-1}{n!}$
=1-$\frac{1}{3！}$+$\frac{3}{4！}$+…+$\frac{n-1}{n!}$
=1-$\frac{1}{n!}$
故答案为：1-$\frac{1}{n!}$．

点评此题考查了排列数公式的应用，熟练掌握运算法则是解本题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

5．

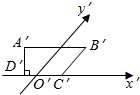如图所示，A′B′C′D′是一个水平放置的平面图形的斜二测直观图，已知A′B′C′D′是一个直角梯形，A′B′∥C′D′，A′D′⊥C′D′，且B′C′与y轴平行，又A′B′=21，DC′′=9，A′D′=12，试求梯形A′B′C′D′的原图形ABCD的面积．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

6．如图，在长方体ABCD-A₁B₁C₁D₁中，求证：面AA₁D₁D∥面BB₁C₁C．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

3．设函数y=|e^x-1|的图象与直线y=$\frac{1}{m+1}$的两交点横坐标分别为x₁、x₂（x₁＜x₂），与直线y=m的两交点横坐标分别为x₃、x₄（x₃＜x₄），若m∈（0，$\frac{1}{2}$），则（x₄+x₁）-（x₃+x₂）的取值范围是（　　）

A．

（-∞，0）

B．

（-∞，ln$\frac{3}{5}$）

C．

（ln$\frac{3}{5}$，0）

D．

（-∞，-1）

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

10．对于定义在R上的函数f（x），有下述四个命题；
①若y=f（x）是奇函数，则y=f（x-1）的图象关于点A（1，0）对称；
②若函数y=f（x+1）与y=f（1-x）的图象关于直线x=1对称；
③如果函数y=f（x）满足f（x+1）=f（1-x），f（x+3）=f（3-x），那么该函数以4为周期．
其中正确命题的序号为①③．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

20．若$\sqrt{4{a}^{2}-4a+1}$=$\root{3}{（1-2a）^{3}}$，则实数a的取值范围是（　　）

A．

a∈R

B．

a=$\frac{1}{2}$

C．

a＞$\frac{1}{2}$

D．

a≤$\frac{1}{2}$

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

7．已知向量$\overrightarrow{a}$=（3，-4），$\overrightarrow{a}$⊥$\overrightarrow{b}$，则向量$\overrightarrow{b}$的单位向量的坐标是（$\frac{4}{5}$，$\frac{3}{5}$）或（-$\frac{4}{5}$，-$\frac{3}{5}$）．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

4．设全集U={3，6，m²-m-1}，A={|3-2m|，6}，∁_UA={5}，求实数m．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

15．已知函数g（x）=sinx+acosx+2017满足g（x）+g（$\frac{7π}{3}$-x）=4034，又f（x）=asinx+cosx对任意x恒有f（x）≤|f（x₀）|，则满足条件的x₀可以是（　　）

A．

$\frac{π}{3}$

B．

$\frac{π}{4}$

C．

$\frac{5π}{6}$