
| A. | (e,+∞) | B. | (1,e) | C. | (-∞,-e) | D. | (-e,-1) |
分析 依题意知-k=f(f(x))=$\left\{\begin{array}{l}{{e}^{{e}^{x}},x≥0}\\{{e}^{-2x},x<0}\end{array}\right.$,x≥0,${e}^{{e}^{x}}$≥e,x<0,e-2x>1,根据函数g(x)=f(f(x))+k在x∈R上有且仅有一个零点,即可得出结论.
解答 解:依题意知-k=f(f(x))=$\left\{\begin{array}{l}{{e}^{{e}^{x}},x≥0}\\{{e}^{-2x},x<0}\end{array}\right.$,
x≥0,${e}^{{e}^{x}}$≥e,x<0,e-2x>1,
∵函数g(x)=f(f(x))+k在x∈R上有且仅有一个零点,
∴1<-k<e,∴-e<k<-1,
故选:D.
点评 本题考查分段函数,考查函数的零点,考查学生分析解决问题的能力,正确求出分段函数是关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -x(1-x) | B. | x(1-x) | C. | -x(1+x) | D. | x(1+x) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x(℃) | 300 | 400 | 500 | 600 | 700 | 800 |
| y(%) | 40 | 50 | 55 | 60 | 67 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,\frac{3}{2}]$ | B. | $[\frac{3}{2},+∞)$ | C. | (-∞,-1] | D. | [4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
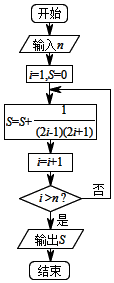
| A. | $\frac{4}{9}$ | B. | $\frac{8}{9}$ | C. | $\frac{3}{7}$ | D. | $\frac{6}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
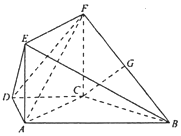 如图,在梯形ABCD中,AB∥CD,AB=4,AD=DC=CB=2,四边形ACFE是矩形,AE=1,平面ACFE⊥平面ABCD,点G是BF的中点.
如图,在梯形ABCD中,AB∥CD,AB=4,AD=DC=CB=2,四边形ACFE是矩形,AE=1,平面ACFE⊥平面ABCD,点G是BF的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com