
分析 (Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(Ⅱ)问题等价于“对于任意x∈[0,2],f(x)min≥g(x)max成立”,根据函数的单调性求出a的范围即可.
解答 解:(Ⅰ)函数f(x)的定义域为R,$f'(x)=\frac{{(1-{x^2})}}{{{{({x^2}+1)}^2}}}=\frac{(1-x)(1+x)}{{{{({x^2}+1)}^2}}}$.…(2分)
当x变化时,f'(x),f(x)的变化情况如下表:
| x | (-∞,-1) | (-1,1) | (1,+∞) |
| f'(x) | - | + | - |
| f(x) | ↘ | ↗ | ↘ |
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想、转化思想,是一道综合题.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:选择题
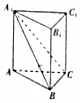 如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1B1BA,且AA1=AB=BC=2,则AC与平面A1BC所成角为( )
如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1B1BA,且AA1=AB=BC=2,则AC与平面A1BC所成角为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为监测全市小学生身体形态生理机能的指标情况,体检中心从某小学随机抽取100名学生,将他们的身高(单位:厘米)数据分成如下5个组:[100,110),[110,120),…,[140,150),并绘制成频率分布直方图(如图所示).
为监测全市小学生身体形态生理机能的指标情况,体检中心从某小学随机抽取100名学生,将他们的身高(单位:厘米)数据分成如下5个组:[100,110),[110,120),…,[140,150),并绘制成频率分布直方图(如图所示).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x<0,x2-2x+1≥0 | B. | ?x≤0,x2-2x+1>0 | C. | ?x>0,x2-2x+1≥0 | D. | ?x>0,x2-2x+1<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (e,+∞) | B. | (1,e) | C. | (-∞,-e) | D. | (-e,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com