已知f(x)=x3+ax2-a2x+2.
(Ⅰ)若a=1,求曲线y=f(x)在点(1,f(1)处的切线方程;
(Ⅱ)若a≠0 求函数f(x)的单调区间;
(Ⅲ)若不等式2xlnx≤f′(x)+a2+1恒成立,求实数a的取值范围.
解:(Ⅰ)∵a=1,∴f(x)=x
3+x
2-x+2,
∴f′(x)=3x
2+2x-1,∴k=f′(1)=4,又f(1)=3,所有切点坐标为(1,3).
∴所求切线方程为y-3=4(x-1),即4x-y-1=0.
(Ⅱ)f′(x)=3x
2+2ax-a
2=(x+a)(3x-a)由f′(x)=0,得x=-a或x=

.
(1)当a>0时,由f′(x)<0,得-a<x<

;由f′(x)>0,得x<-a或x>

,
此时f(x)的单调递减区间为(-a,

),单调递增区间为(-∞,-a)和(

,+∞).
(2)当a<0时,由f′(x)<0,得
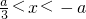
;由f′(x)>0,得x<

或x>-a.
此时f(x)的单调递减区间为(

,-a),单调递增区间为(-∞,

)和(-a,+∞).
综上:当a>0时,f(x)的单调递减区间为(-a,

),单调递增区间为(-∞,-a)和(

,+∞);
当a<0时,f(x)的单调递减区间为(

,-a),单调递增区间为(-∞,

)和(-a,+∞).
(Ⅲ)依题意x∈(0,+∞),不等式2xlnx≤f′(x)+a
2+1恒成立,
等价于2xlnx≤3x
2+2ax+1在(0,+∞)上恒成立,可得a≥lnx-

x-

在(0,+∞)上恒成立,
设h(x)=lnx-
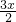
-

,则h′(x)=

-

+
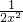
=-

.
令h′(x)=0,得x=1,x=-

(舍),当0<x<1时,h′(x)>0;当x>1时,h′(x)<0,
当x变化时,h′(x),h(x)变化情况如下表:
| x | (0,1) | 1 | (1,+∞) |
| h′(x) | + | 0 | - |
| h(x) | 单调递增 | -2 | 单调递减 |
∴当x=1时,h(x)取得最大值,h(x)
max=-2,∴a≥-2.
∴a的取值范围是[-2,+∞).
分析:(Ⅰ)求出切点坐标,斜率k,k=f′(1),用点斜式即可求出方程;
(Ⅱ)解含参的不等式:f′(x)>0,f′(x)<0即可;
(Ⅲ)分离出参数a后,转化为函数的最值问题解决,注意函数定义域.
点评:本题考查了导数的几何意义、应用导数研究函数的单调性、求函数最值问题,不等式恒成立常转化为函数最值问题解决.

 .
. ;由f′(x)>0,得x<-a或x>
;由f′(x)>0,得x<-a或x> ,
, ),单调递增区间为(-∞,-a)和(
),单调递增区间为(-∞,-a)和( ,+∞).
,+∞).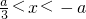 ;由f′(x)>0,得x<
;由f′(x)>0,得x< 或x>-a.
或x>-a. ,-a),单调递增区间为(-∞,
,-a),单调递增区间为(-∞, )和(-a,+∞).
)和(-a,+∞). ),单调递增区间为(-∞,-a)和(
),单调递增区间为(-∞,-a)和( ,+∞);
,+∞); ,-a),单调递增区间为(-∞,
,-a),单调递增区间为(-∞, )和(-a,+∞).
)和(-a,+∞). x-
x- 在(0,+∞)上恒成立,
在(0,+∞)上恒成立,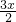 -
- ,则h′(x)=
,则h′(x)= -
- +
+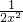 =-
=- .
. (舍),当0<x<1时,h′(x)>0;当x>1时,h′(x)<0,
(舍),当0<x<1时,h′(x)>0;当x>1时,h′(x)<0,

 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案